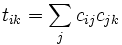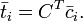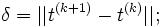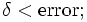EigenTrust
|
|
Este artículo posiblemente contiene investigación original. (Diciembre de 2011) |
|
|
Este artículo también puede ser técnica para la mayoría de los lectores a entender. (Diciembre de 2011) |
EigenTrust algoritmo es un gestión de la reputación algoritmo para el Peer-to-peer redes, desarrolladas por Sep Kamvar, Mario Schlosser, y Hector Garcia-Molina. El algoritmo proporciona cada peer en la red un valor único Fiduciario global basado en la historia de los pares de cargas y así pretende reducir el número de archivos inauténtico en un P2P red.
Contenido
- 1 Resumen
- 2 Algoritmo
- 3 Véase también
- 4 Referencias
Resumen
Peer-to-peer sistemas disponibles hoy en día (como Gnutella) son abiertas, a menudo anónimo y falta de rendición de cuentas. Por lo tanto, un usuario malicioso puede introducir en los recursos de red peer-to-peer que pueden ser (inauténtica, corruptos o maliciosoVirus). Esto refleja mal la credibilidad de los actuales sistemas peer-to-peer. Un equipo de investigadores de Stanford proporciona un sistema de gestión de reputación, donde cada par en el sistema tiene un valor de confianza global único basado en la historia de los pares de cargas. Cualquier par solicitar recursos podrán tener acceso al valor de la confianza de un compañero y evitar la descarga de archivos de pares no es de confianza.
Algoritmo
El algoritmo de Eigentrust se basa en la noción de confianza transitiva: Si un colega i Confía en cualquier par j, también se confía en la confianza de los pares j. Cada par i calcula el valor local de confianza sij para todos los participantes han proporcionado con descargas auténticos o falsos basados en las transacciones satisfactorias o insatisfactorias que ha tenido.
¿Dónde se sentó)i, j) se refiere al número de respuestas satisfactorias que pares i ha recibido de peer jy unsat ()i,j) se refiere al número de respuestas insatisfactorias que pares i ha recibido de peer j.
Se normaliza el valor local, para prevenir a malintencionados compañeros de asignar valores arbitrariamente alta confianza local a conspirar pares maliciosos y arbitrariamente bajo los valores de confianza local a Buenos compañeros. El valor normalizado confianza local cij es entonces
Los valores fiduciarios local se agregan en una ubicación central o de manera distribuida para crear un vector de confianza para toda la red. Basado en la idea de relaciones de confianza transitivas, un compañero i pediría a otros compañeros sabe a declarar el valor de la confianza de un compañero k y pesan las respuestas de estos pares por el interlocutor de confianza i lugares en ellos.
Si suponemos que un usuario sabía el cij los valores de toda la red en forma de un matriz C, entonces vector de confianza 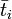 define el valor de la confianza para
define el valor de la confianza para  está dada por
está dada por
En la ecuación mostrada anteriormente, si C se supone para ser aperiódica y fuertemente conectados, poderes de la matriz C se reunirán en un valor estable en algún momento.
Parece que para un valor grande de x, el vector de confianza 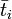 se reunirán al mismo vector para todos los pares en la red. El vector
se reunirán al mismo vector para todos los pares en la red. El vector 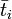 es conocido como el izquierda[aclarar] principal cuadráticos de la matriz C. Además tenemos en cuenta que desde
es conocido como el izquierda[aclarar] principal cuadráticos de la matriz C. Además tenemos en cuenta que desde 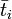 es igual para todos los nodos de la red, que representa el valor global de confianza.
es igual para todos los nodos de la red, que representa el valor global de confianza.
Basándose en los resultados por encima del valor confianza centralizado simple algoritmo informático puede escribirse. Tenga en cuenta que suponemos que todos los valores de confianza local para toda la red están disponibles y presentes en la matriz C. También tomamos nota de que, si la ecuación que se muestra arriba converge, podemos reemplazar el vector inicial  por un vector
por un vector 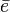 es un m-vector representación uniforme distribución de probabilidad sobre todo m pares. A continuación se muestra el algoritmo básico de EigenTrust:
es un m-vector representación uniforme distribución de probabilidad sobre todo m pares. A continuación se muestra el algoritmo básico de EigenTrust:
- repetir
-
hasta
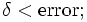
Véase también
- Cadena de Markov
- Autovalores y autovectores en matemáticas y física
- Eigen (biblioteca de C++), una biblioteca de programación de computadoras para las operaciones de matriz y álgebra lineal
Referencias
- S. D. Kamvar, M. T. Schlosser y H. Garcia-Molina, el algoritmo de EigenTrust para la gestión de la reputación en las redes P2P, en actas del XII Congreso Internacional World Wide Web, 2003.
Otras Páginas
- LongRun
- Dorfbahn Serfaus
- Broker de negocios
- Webnode
- Hablando de terapias
- Cuidado de la salud con fondos propios
- Datos de Object Management Group
- Municipalidad Local Tswelopele
- BMW M12
- Biblioteca del Congreso de clasificacion: clase D, subclase D--Historia General
- Balonmano Cercle Nimes
- Asbesto (categoria todos los articulos con declaraciones promocionales)
- Tractor de ciudad
- Control de compromiso
- Cita (pelicula de 1935)
- Mirar al trasluz del oido
- Swap de credito predeterminado (seccion de liquidacion)
- Cierto que