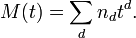Serie de Molien
En Matemáticastt Serie de Molien es un función generatriz conectado a un representación lineal Ρ de un Grupo G en un espacio finito-dimensional del vector V. Cuenta con la polinomios homogéneos de un determinado grado total d son invariantes para G. Se nombra para Theodor Molien.
Contenido
- 1 Formulación
- 2 Fórmula
- 3 Ejemplo
- 4 Referencias
Formulación
Más formalmente, hay un espacio del vector de estos polinomios, para cada valor dado de d = 0, 1, 2,... y nos escriben nd para su espacio vectorial de dimensión, o en otras palabras el número de invariantes homogéneos linealmente independientes de un grado determinado. En términos más algebraicas, tome la d-ésimo alimentación simétrica de Vy la representación de G derivados por ρ. Los invariantes forman el subespacio de todos los vectores fijados por todos los elementos de G, y nd es su dimensión.
La serie de Molien es entonces por definición la serie de energía formal
Esto puede ser mirado de otra manera, teniendo en cuenta la representación de G en el Álgebra simétrica de Vy entonces el conjunto bajoálgebra R de G-invariantes. Entonces nd es la dimensión de la parte homogénea de la R de la dimensión d, cuando lo miramos como anillo graduado. De esta manera una serie de Molien es también una especie de Función de Hilbert. Sin más hipótesis no mucho se pueden decir, pero suponiendo que ciertas condiciones de finitud es posible demostrar que la serie de Molien es un función racional. El caso de grupos finitos se estudia más a menudo.
Fórmula
Molien demostró que
Esto significa que el coeficiente de td en esta serie es la dimensión nd definido anteriormente. Asume que la característica del campo no se divide |G| (pero aun sin esta hipótesis, fórmula de Molien en forma  es válido, aunque no ayuda con la informática M(t)).
es válido, aunque no ayuda con la informática M(t)).
Ejemplo
Tener en cuenta 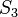 actuando sobre R3 por permutando las coordenadas. Tenga en cuenta que
actuando sobre R3 por permutando las coordenadas. Tenga en cuenta que  es constante en las clases de GACION, así que es suficiente para tomar uno de cada una de las tres clases de
es constante en las clases de GACION, así que es suficiente para tomar uno de cada una de las tres clases de 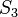 ; por lo que
; por lo que  y
y  donde
donde  y
y  .
.
Entonces
Referencias
- David A. Cox, John B. poco, Donal o ' Shea (2005), Usando geometría algebraica, págs. 295-8
- Molien, TH. (1897). "Uber die Invarianten der linearen Substitutionsgruppen.". Sitzungber. KONIG. Preuss. Akad. Wiss. (J. Berl. BER.) 52:: 1152-1156. SI ES.28.0115.01.
- Mukai, S. (2002). Una introducción a invariantes y módulos. Estudios de Cambridge en matemáticas avanzadas 81. ISBN978-0-521-80906-1.