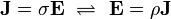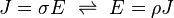Conductividad y resistividad eléctrica
Resistividad eléctrica (también conocido como resistividad, resistencia eléctrica específica, o resistividad de volumen) es una propiedad intrínseca que cuantifica un determinado material opone como fuertemente el flujo de corriente eléctrica. Una baja resistividad indica un material que permite fácilmente el movimiento de carga eléctrica. Resistividad es comúnmente representado por el Letra griega (ΡRho). El SI unidad de resistencia eléctrica es la Ohm⋅metro (Ω⋅m)[1][2][3] Aunque otras unidades como Ohm⋅centímetro (Ω⋅cm) también se encuentran en uso. Por ejemplo, si un 1 m x 1 m x 1 m cubo sólido de material tiene hoja contactos en dos caras opuestas y la resistencia entre estos contactos es 1 Ω, entonces la resistencia del material es 1 Ω⋅m.
Conductividad eléctrica o conductancia específica es el recíproco de la resistencia eléctrica, y mide la habilidad de un material para llevar a cabo una corriente eléctrica. Es comúnmente representado por la letra griega σ (Sigma), pero (κKappa) (especialmente en ingeniería eléctrica) o (γ)gamma) se utilizan ocasionalmente. Su unidad es Siemens por metro (S/m) y Unidad de GCEP es recíproco segundo (s−1).
Contenido
- 1 Definición
- 1.1 Resistencias o conductores con sección transversal uniforme
- 1.2 Definición general
- 2 Causas de la conductividad
- 2.1 Teoría de banda simplificada
- 2.2 En metales
- 2.3 En semiconductores y aisladores
- 2.4 En líquidos iónicos/electrolitos
- 2.5 Superconductividad
- 2.6 Plasma
- 3 Resistencia de materiales diversos
- 4 Dependencia de la temperatura
- 4.1 Aproximación lineal
- 4.2 Metales
- 4.3 Semiconductores
- 5 Conductividad y resistividad compleja
- 6 Ecuaciones del tensor para materiales anisótropos
- 7 Resistencia contra resistencia en geometrías complicadas
- 8 Productos de densidad de resistividad
- 9 Véase también
- 10 Notas
- 11 Referencias
- 12 Lectura adicional
- 13 Enlaces externos
Definición
Resistencias o conductores con sección transversal uniforme

Muchos resistencias y conductores tienen una sección transversal uniforme con un flujo uniforme de la corriente eléctrica y están hechas de un material. (Vea el diagrama a la derecha). En este caso, la resistividad eléctrica ρ (Griego: Rho) se define como:
donde
- R es el resistencia eléctrica de una muestra uniforme del material (medido en ohmiosΩ).
-
 es el longitud de la pieza de material (medido en metrosm).
es el longitud de la pieza de material (medido en metrosm).
- A es el área transversal de la muestra (medida en metros cuadrados, m 2).
La razón por la resistividad se define de esta manera es que hace resistencia una propiedad intrínseca, a diferencia de la resistencia. Todos los alambres de cobre, independientemente de su forma y tamaño, tienen aproximadamente el mismo resistividad, pero un largo y delgado hilo de cobre tiene un mucho mayor resistencia que un alambre de cobre grueso y corto. Cada material tiene su propia resistencia característica – por ejemplo, la resistencia del caucho es mucho mayor que la del cobre.
En un analogía hidráulica, paso actual a través de un material de alta resistividad es como empujar el agua a través de un tubo lleno de arena, mientras que el paso actual a través de un material de baja resistividad es como empujar el agua a través de un tubo vacío. Si los tubos son del mismo tamaño y forma, los tubos llenos de arena tiene mayor resistencia al flujo. Pero la resistencia no únicamente determinada por la presencia o ausencia de la arena; también depende de la longitud y anchura de la pipa: tubos cortos o amplia tendrá menor resistencia que las tuberías estrechas o largas.
La ecuación anterior puede ser transpuesta para obtener Ley de Pouillet (el nombre de Claude Pouillet):
La resistencia de un determinado material se aumentan con la longitud, pero disminuye con el aumento de la superficie transversal. De las ecuaciones anteriores, tiene resistencia SI unidades de Ohm⋅metro. A veces también se utilizan otras unidades como ohm⋅cm o ohm⋅inch.
La fórmula  puede utilizarse para entender intuitivamente el significado de un valor de resistividad. Por ejemplo, si
puede utilizarse para entender intuitivamente el significado de un valor de resistividad. Por ejemplo, si  y
y  (formando un cubo con contactos perfectamente conductora en caras opuestas), entonces la resistencia de este elemento en ohmios es numéricamente igual a la resistencia del material está constituido en ohmios-metros. Asimismo, un material ohm⋅cm 1 tendría una resistencia de 1 ohmio si entra en contacto en caras opuestas de un cubo de 1 cm × 1 cm × 1 cm.
(formando un cubo con contactos perfectamente conductora en caras opuestas), entonces la resistencia de este elemento en ohmios es numéricamente igual a la resistencia del material está constituido en ohmios-metros. Asimismo, un material ohm⋅cm 1 tendría una resistencia de 1 ohmio si entra en contacto en caras opuestas de un cubo de 1 cm × 1 cm × 1 cm.
Conductividad σ (Griego: Sigma) se define como el inverso de la resistividad:
Conductividad tiene unidades de Siemens por metro (S/m).
Definición general
La definición anterior fue específica para resistencias o conductores de sección uniforme, donde la corriente fluye uniformemente a través de ellos. Una definición más básica y general inicia desde el hecho eso si hay campo eléctrico dentro de un material, que provocará corriente eléctrica a fluir. La resistividad eléctrica ρ se define como la relación entre el campo eléctrico a la densidad de la corriente que se crea:
donde
- ρ es la resistividad del material conductor (medido en ohm⋅metres, Ω⋅m),
- E es el magnitud de la campo eléctrico (en voltios por metroV⋅m −1),
- J es la magnitud de la densidad de corriente (en amperios por metro cuadradoA⋅m −2),
en el cual E y J están dentro del conductor.
La conductividad es la inversa:
Por ejemplo, el caucho es un material con grandes ρ y pequeños σ, porque incluso un campo eléctrico muy grande en goma no hará que casi ninguna corriente fluyendo a través de él. Por otro lado, el cobre es un material con pequeñas ρ y grandes σ, porque incluso un pequeño campo eléctrico tira mucho de la corriente a través de él.
Causas de la conductividad
Teoría de banda simplificada

Mecánica cuántica Estados que los electrones en un átomo no pueden tomar cualquier valor arbitrario de energía. Por el contrario, existen niveles de energía fija que los electrones pueden ocupar, y valores entre estos niveles son imposibles. Cuando permitió a un gran número de tales niveles de energía están espaciados juntos (en energía-espacio), es decir, tiene energías similares (minuciosamente diferentes), entonces podemos hablar de estos niveles de energía como una "banda de energía". Puede haber muchas tales bandas de energía en un material, según el número atómico (número de electrones) y su distribución (además de factores externos como el ambiente modificando las bandas de energía).
Los electrones del material tratan de minimizar la energía total en el material por ir a los Estados de baja energía; Sin embargo, la Principio de exclusión de Pauli significa que no todos pueden ir al estado más bajo. Los electrones en lugar de otro "llenan" la estructura de la banda a partir de la parte inferior. El nivel de energía característico hasta que han llenado los electrones se denomina el Nivel de Fermi. La posición del nivel de Fermi respecto a la estructura de la banda es muy importante para la conducción eléctrica: sólo los electrones en los niveles de energía cerca de la Nivel de Fermi son libres para moverse, ya que los electrones pueden saltar fácilmente entre los Estados parcialmente ocupados en esa región. En contraste, los Estados de baja energía rígidamente están llenos de un número fijo de electrones en todo momento, y los Estados de alta energía están vacíos de electrones en todo momento.
En metales existen muchos niveles de energía cerca del nivel de Fermi, lo que significa que hay muchos electrones disponibles para moverse. Esto es lo que causa la alta conductividad electrónica en metales.
Una parte importante de la teoría de la banda es que allí puede ser prohibido bandas de energía: intervalos de energía que no contienen ningún niveles de energía. En aisladores y semiconductores, el número de electrones pasa a ser apenas la cantidad correcta para llenar un cierto número entero de bandas de energía baja, exactamente a la frontera. En este caso, el nivel de Fermi cae dentro de una banda prohibida. Puesto que no no hay Estados disponibles cerca del nivel de Fermi, y los electrones no son libremente móviles, la conductividad electrónica es muy baja.
En metales

A metal consiste en un enrejado de átomos, cada uno con una cáscara externa de electrones que libremente disociar de los átomos de su padre y viajar a través de la celosía. Esto también es conocido como un enrejado iónico positivo.[4] Este 'mar' de electrones puede disociables permite el metal conducir la corriente eléctrica. Cuando una eléctrica diferencia de potencial (una voltaje) se aplica a través del metal, la resultante campo eléctrico provoca que los electrones a la deriva hacia el terminal positivo. El real velocidad de deriva de los electrones son muy pequeños, del orden de magnitud de un metro por hora. Sin embargo, como los electrones están densamente poblados en el material, el campo electromagnético es propaga a través del metal en el velocidad de la luz.[5] El mecanismo es similar a la transferencia del impulso de bolas en un Cuna de Newton.[6]
Cerca de temperatura ambiente, metales, tienen resistencia. La principal causa de esta resistencia es la colisión de los electrones con los átomos que componen el enrejado cristalino. Esto actúa a electrones de dispersión y pierden su energía en las colisiones en lugar de movimiento lineal a través de la latice. También contribuyen a la resistencia en metales con impurezas es las imperfecciones resultantes en el enrejado.[7]
Cuanto mayor sea el área transversal del conductor, los electrones más por unidad de longitud están disponibles para llevar la corriente. Como resultado, la resistencia es menor en los conductores de sección transversal más grandes. El número de eventos de dispersión encontradas por un electrón pasa a través de un material es proporcional a la longitud del conductor. Cuanto más tiempo el conductor, por lo tanto, cuanto mayor sea la resistencia. Diferentes materiales también afectan a la resistencia.[8]
En semiconductores y aisladores
En metales, el Nivel de Fermi se encuentra en la banda de conducción (véase teoría de la banda, arriba) dando lugar a liberar electrones de la conducción. Sin embargo, en semiconductores la posición del nivel de Fermi está dentro de la banda prohibida, aproximadamente a medio camino entre el mínimo de la banda de conducción y banda de Valencia máxima para los semiconductores intrínsecos (lámpara). Esto significa que a 0 grados kelvin, hay no hay electrones de la conducción libre y la resistencia es infinita. Sin embargo, la resistencia continuará disminuye a medida que la densidad del portador de carga en los aumentos de la banda de conducción. En semiconductores extrínsecos (dopados), dopante átomos de aumentarán la concentración de portador de carga mayoría donar electrones a la banda de conducción o aceptando los agujeros en la banda de Valencia. Para ambos tipos de donantes o aceptador de átomos, aumentando la densidad del dopante conduce a una reducción en la resistencia, por lo tanto altamente dopados semiconductores se comportan metálico. A muy altas temperaturas, la contribución de los portadores generados térmicamente predominará sobre la contribución de los átomos dopante y disminuirá la resistencia exponencialmente con la temperatura.
En líquidos iónicos/electrolitos
En electrólitos, conducción eléctrica ocurre no por los electrones de la banda o agujeros, sino por especies completo atómico (iones) viajando, cada uno llevando una carga eléctrica. La resistividad de líquidos iónicos varía enormemente por la concentración – mientras que el agua destilada es casi un aislador, agua salada es un conductor eléctrico muy eficiente. En membranas biológicas, las corrientes son llevadas por sales iónicas. Pequeños agujeros en las membranas, llamados canales iónicos, son selectivos a iones específicos y determinar la resistencia de la membrana.
Superconductividad
La resistividad eléctrica de un metal conductor disminuye gradualmente a medida que desciende la temperatura. En ordinario conductores, tales como cobre o plata, esta disminución se ve limitada por las impurezas y otros defectos. Incluso cerca cero absoluto, una muestra real de un conductor normal muestra cierta resistencia. En un superconductor, la resistencia baja abruptamente a cero cuando el material se enfría por debajo de su temperatura crítica. Un corriente eléctrica que fluye en un bucle de cables superconductores puede persistir indefinidamente sin fuente de energía.[9]
En 1986, se descubrió que algunos cuprato-perovskita cerámica los materiales tienen una temperatura crítica superior a 90 K (−183 ° C). Tal temperatura alta transición es teóricamente imposible para un superconductor convencional, llevando los materiales a denominarse superconductores de alta temperatura. Nitrógeno líquido hierve a 77 K, facilitar muchos experimentos y aplicaciones que son menos prácticas en temperaturas más bajas. En los superconductores convencionales, los electrones se mantienen Unidas en pares por una atracción mediada por enrejado fonones. El mejor modelo disponible de superconductividad de alta temperatura es todavía algo tosca. Hay una hipótesis que emparejamiento de electrones en los superconductores de alta temperatura es mediada por olas de centrifugado corto alcance conocidas como paramagnons.[10]
Plasma

Plasmas son muy buenos conductores eléctricos y potenciales eléctricos juegan un papel importante. El potencial que existe en promedio en el espacio entre partículas cargadas, independientes de la cuestión de cómo se puede medir, se llama el "potencial de plasma", o el "espacio potencial". Si un electrodo se inserta en un plasma, su potencial generalmente se acostará considerablemente por debajo del potencial debido a lo que se denomina plasma un Vaina Debye. La buena conductividad eléctrica de plasmas hace sus campos eléctricos muy pequeños. Esto se traduce en el importante concepto de "quasineutrality", que dice que la densidad de cargas negativas es aproximadamente igual a la densidad de cargas positivas sobre grandes volúmenes de la (plasmane= < Z >ni), pero en la escala de la Longitud de Debye puede haber un desequilibrio de la carga. En el especial del caso capas dobles son formadas, la separación del cargo puede extender algunas decenas de Debye longitudes.
La magnitud de las potencialidades y los campos eléctricos debe ser determinada por medios que no sean simplemente encontrar la red densidad de la carga. Un ejemplo común es suponer que los electrones cumplen la Relación de Boltzmann:
Diferenciar a esta relación proporciona un medio para calcular el campo eléctrico de la densidad:
Es posible producir un plasma que no es quasineutral. Un haz de electrones, por ejemplo, tiene solamente cargas negativas. La densidad de un plasma no neutral debe ser generalmente muy baja, o debe ser muy pequeño, de lo contrario se disiparán por el repulsivo fuerza electrostática.
En Astrofísica plasmas, Proyección de Debye evita campos eléctricos desde que afectan directamente el plasma a grandes distancias, es decir, mayor que el Longitud de Debye. Sin embargo, la existencia de partículas cargadas provoca el plasma generar y ser afectado por campos magnéticos. Esto puede y causa un comportamiento extremadamente complejo, como la generación de las capas dobles de plasma, un objeto que separa carga sobre unas pocas decenas de Longitud de Debye. La dinámica de las plasmas interactuando con externos y autogenerado campos magnéticos se estudian en el disciplina académica de magnetohidrodinámica.
Plasma es a menudo llamado el cuarto estado de la materia después de sólidos, líquidos y gases.[12][13] Es distinta de éstas y otras fuentes de energía más baja Estados de la materia. Aunque está estrechamente relacionada a la fase de gas en eso también tiene una forma definida ni volumen, difiere en muchas formas, incluyendo las siguientes:
| Propiedad | Gas | Plasma |
|---|---|---|
| Conductividad eléctrica | Muy baja:: Aire es un excelente aislante hasta que se descompone en plasma a intensidades de campo eléctrico por encima de 30 kilovoltios por centímetro.[14] | Suele ser muy alta:: Para muchos propósitos, la conductividad de un plasma puede ser tratada como infinito. |
| Actuando independientemente de las especies | Uno:: Todas las partículas del gas se comportan de manera similar, influenciada por gravedad y por colisiones uno con el otro. | Dos o tres: Electrones, iones, protones y neutrones se pueden distinguir por el signo y el valor de sus carga Así se comportan independientemente en muchas circunstancias, con velocidades diferentes a granel y las temperaturas, permitiendo que los fenómenos tales como nuevos tipos de olas y inestabilidades. |
| Distribución de velocidad | Maxweliana:: Colisiones conducen generalmente a una distribución de velocidad Maxweliana de todas las partículas de gas, con muy pocas partículas relativamente rápidas. | A menudo no-Maxweliana:: Interacciones inicar a menudo son débiles en plasmas calientes y forzamiento externo puede conducir el plasma lejos de equilibrio local y conducir a una población significativa de partículas inusualmente rápidas. |
| Interacciones | Binario:: Dos partículas colisiones son la regla, tres cuerpos colisiones extremadamente raras. | Colectivo:: Ondas, o movimiento organizado de plasma, son muy importantes porque las partículas pueden interactuar a largas distancias a través de fuerzas magnéticas y eléctricas. |
Resistencia de materiales diversos
- A conductor tales como un metal tiene alta conductividad y una baja resistividad.
- Un aislador como vidrio tiene baja conductividad y una alta resistividad.
- La conductividad de una semiconductor es generalmente intermedia, pero varía ampliamente en diferentes condiciones, tales como la exposición del material a campos eléctricos o frecuencias específicas de luzy, más importante, con temperatura y la composición del material semiconductor.
El grado de dopaje en semiconductores hace una gran diferencia en la conductividad. A un punto de dopaje más conduce a mayor conductividad. La conductividad de una solución de agua es altamente dependiente de su concentración de disuelto Salesy otras especies químicas que ionizar en la solución. Conductividad eléctrica de muestras de agua se utiliza como un indicador de cómo sal-libre, libre de iones, o libre de impureza es la muestra; el más puro del agua, menor la conductividad (cuanto mayor sea la resistividad). Las mediciones de conductividad en el agua a menudo se presentan como conductancia específica, en relación a la conductividad del agua pura en 25 ° C. Un Medidor EC normalmente se utiliza para medir la conductividad de una solución. Un áspero Resumen es el siguiente:
| Material | Resistividad Ρ (Ω·m) |
| Superconductores | 0 |
| Metales | 10−8 |
| Semiconductores | variable |
| Electrólitos | variable |
| Aisladores | 1016 |
Esta tabla muestra la resistividad, conductividad y coeficiente de temperatura de los distintos materiales a 20° C (68 ° F293 K)
| Material | Ρ (Ω·m) en 20 ° C | Σ (S/m) en 20 ° C | Temperatura coeficiente[Nota 1] (K−1) |
Referencia |
|---|---|---|---|---|
| Carbono (el grafeno) | 1.00×10−8 | - | -0.0002 | [15] |
| Plata | 1.59×10−8 | 6.30×107 | 0.0038 | [16][17] |
| Cobre | 1.68×10−8 | 5,96×107 | 0.003862 | [18] |
| Recocido cobre[Nota 2] | 1,72×10−8 | 5,80×107 | 0.00393 | [19] |
| Oro[Nota 3] | 2.44×10−8 | 4.10×107 | 0.0034 | [16] |
| Aluminio[Nota 4] | 2.82×10−8 | 3.50×107 | 0.0039 | [16] |
| Calcio | 3.36×10−8 | 2.98×107 | 0.0041 | |
| Tungsteno | 5.60×10−8 | 1.79×107 | 0.0045 | [16] |
| Cinc | 5,90×10−8 | 1.69×107 | 0.0037 | [20] |
| Níquel | 6.99×10−8 | 1.43×107 | 0.006 | |
| Litio | 9,28×10−8 | 1.08×107 | 0.006 | |
| Hierro | 1.00×10−7 | 1.00×107 | 0.005 | [16] |
| Platino | 1.06×10−7 | 9,43×106 | 0,00392 | [16] |
| Lata | 1.09×10−7 | 9.17×106 | 0.0045 | |
| Acero al carbono (1010) | 1.43×10−7 | 6.99×106 | [21] | |
| Plomo | 2.20×10−7 | 4.55×106 | 0.0039 | [16] |
| Titanio | 4.20×10−7 | 2.38×106 | X | |
| Grano orientado acero eléctrico | 4,60×10−7 | 2.17×106 | [22] | |
| Manganina | 4,82×10−7 | 2.07×106 | 0.000002 | [23] |
| Constantan | 4,90×10−7 | 2.04×106 | 0.000008 | [24] |
| Acero inoxidable[Nota 5] | 6,90×10−7 | 1.45×106 | [25] | |
| Mercurio | 9,80×10−7 | 1.02×106 | 0.0009 | [23] |
| Nicrom[Nota 6] | 1.10×10−6 | 9.09×105 | 0.0004 | [16] |
| GaAs | 1.00×10−3 Para 1.00×108 | 1.00×10−8 Para 103 | [26] | |
| Carbono (amorfo) | 5.00×10−4 Para 8.00×10−4 | 1.25×103 Para 2×103 | −0.0005 | [16][27] |
| Carbono (grafito)[Nota 7] | 2.50×10−6 Para 5.00×10−6 //plano basal 3.00×10−3 Avión ⊥basal |
2.00×105 Para 3.00×105 plano basal 3.30×102 Avión ⊥basal |
[28] | |
| Carbono (diamante) | 1.00×1012 | ~10−13 | [29] | |
| Germanio[Nota 8] | 4,60×10−1 | 2.17 | −0.048 | [16][17] |
| Agua de mar[Nota 9] | 2.00×10−1 | 4,80 | [30] | |
| Agua potable[Nota 10] | 2.00×101 Para 2.00×103 | 5.00×10−4 Para 5.00×10−2 | [citación necesitada] | |
| Silicio[Nota 8] | 6.40×102 | 1.56×10−3 | −0.075 | [16] |
| Madera (húmedo) | 1.00×103 Para 1.00×104 | 10−4 Para 10−3 | [31] | |
| Agua desionizada[Nota 11] | 1.80×105 | 5.50×10−6 | [32] | |
| Vidrio | 10.0×1010 Para 10.0×1014 | 10−11 Para 10−15 | ? | [16][17] |
| Goma dura | 1.00×1013 | 10−14 | ? | [16] |
| Madera (horno seco) | 1.00×1014 Para 1.00×1016 | 10−16 Para 10−14 | [31] | |
| Azufre | 1.00×1015 | 10−16 | ? | [16] |
| Aire | 1.30×1016 Para 3.30×1016 | 3×10−15 Para 8×10−15 | [33] | |
| PEDOT:PSS | 1.00×10−3 Para 1.00×10−1 | 1×101 Para 1×103 | ? | |
| Cuarzo fundido | 7.50×1017 | 1.30×10−18 | ? | [16] |
| PET | 10.0×1020 | 10−21 | ? | |
| Teflon | 10.0×1022 Para 10.0×1024 | 10−25 Para 10−23 | ? |
El coeficiente de temperatura efectiva varía con el nivel de temperatura y de la pureza del material. El valor de 20 ° C es sólo una aproximación cuando se utiliza a otras temperaturas. Por ejemplo, el coeficiente se convierte en inferior a temperaturas más altas para el cobre, y comúnmente se especifica el valor 0.00427 en 0 ° C.[34]
La extremadamente baja resistividad (alta conductividad) de plata es característico de los metales. George Gamow pulcramente resumió la naturaleza de los tratos de los metales con los electrones en su libro de divulgación de la ciencia, Uno, dos, tres...Infinito (1947): "las sustancias metálicas difieren de todos los demás materiales por el hecho de que las capas externas de sus átomos están enlazados muy libremente, y a menudo que uno de sus electrones libres. Así se llene el interior de un metal con un gran número de electrones sin ataduras que recorrer sin rumbo como una multitud de personas desplazadas. Cuando un alambre de metal se somete a la fuerza eléctrica aplicada en su contrario extremos, estos electrones libres corriendo en la dirección de la fuerza, formando lo que llamamos una corriente eléctrica. " Más técnicamente, el modelo de electrón libre da una descripción básica de flujo de electrones en los metales.
Madera es ampliamente considerado como un muy buen aislante, pero su resistencia es sensible depende del contenido de humedad, con madera húmeda, siendo un factor de por lo menos 1010 peor aislante de secado en horno.[31] En cualquier caso, una tensión suficientemente alta – como el de un rayo o algunas líneas de alta tensión – puede provocar riesgo de avería y electrocución aislamiento incluso con madera seca al parecer.
Dependencia de la temperatura
Aproximación lineal
La resistividad eléctrica de la mayoría de los cambios materiales con la temperatura. Si la temperatura T no varía demasiado, un aproximación lineal se utiliza normalmente:
donde  se llama el coeficiente de temperatura de resistencia,
se llama el coeficiente de temperatura de resistencia,  es una temperatura de referencia fijo (normalmente la temperatura ambiente), y
es una temperatura de referencia fijo (normalmente la temperatura ambiente), y  es la resistividad a temperatura
es la resistividad a temperatura  . El parámetro
. El parámetro  un parámetro empírico dispone de los datos de medición. Porque la aproximación lineal es sólo una aproximación,
un parámetro empírico dispone de los datos de medición. Porque la aproximación lineal es sólo una aproximación,  es diferente para las temperaturas de referencia diferente. Por esta razón es habitual para especificar la temperatura que
es diferente para las temperaturas de referencia diferente. Por esta razón es habitual para especificar la temperatura que  se midió en con un sufijo, tales como
se midió en con un sufijo, tales como  , y la relación sólo se mantiene en un rango de temperaturas alrededor de la referencia.[35] Cuando la temperatura varía en un rango de temperatura grande, el aproximación lineal es insuficiente y deben utilizarse un análisis y una comprensión más detallada.
, y la relación sólo se mantiene en un rango de temperaturas alrededor de la referencia.[35] Cuando la temperatura varía en un rango de temperatura grande, el aproximación lineal es insuficiente y deben utilizarse un análisis y una comprensión más detallada.
Metales
En general, electricidad resistividad de metales aumenta con la temperatura. Electrón –Phonon las interacciones pueden desempeñar un papel clave. A altas temperaturas, la resistencia de un metal aumenta linealmente con la temperatura. Como se reduce la temperatura de un metal, la dependencia de la temperatura de la resistencia sigue una función de temperatura ley de energía. Matemáticamente la dependencia de la temperatura de la resistividad ρ de un metal está dada por la fórmula de Bloch – Grüneisen:
donde  es la resistencia residual debido a defecto de dispersión, es una constante que depende de la velocidad de los electrones en el Superficie de Fermi, la Radio de Debye y la densidad del número de electrones en el metal.
es la resistencia residual debido a defecto de dispersión, es una constante que depende de la velocidad de los electrones en el Superficie de Fermi, la Radio de Debye y la densidad del número de electrones en el metal.  es el Temperatura de Debye como obtenidos de mediciones de resistividad y partidos muy de cerca con los valores de temperatura de Debye obtenidos de mediciones de calor específico. n es un entero que depende de la naturaleza de la interacción:
es el Temperatura de Debye como obtenidos de mediciones de resistividad y partidos muy de cerca con los valores de temperatura de Debye obtenidos de mediciones de calor específico. n es un entero que depende de la naturaleza de la interacción:
- n = 5 implica que la resistencia es debido a la dispersión de electrones por fonones (como es para metales simples)
- n = 3 implica que la resistencia es debido a la dispersión de electrones s-d (como es el caso de los metales de transición)
- n = 2 implica que la resistencia es debido a la interacción electrón – electrón.
Si más de una fuente de dispersión está simultáneamente presente, regla de Matthiessen (primero formulada por Augusto Matthiessen en la década de 1860) [36][37] dice que la resistencia total se puede aproximar sumando varios términos diferentes, cada una con el valor adecuado de n.
Como la temperatura del metal es lo suficientemente reducida (para 'congelar' todos los fonones), la resistencia generalmente alcanza un valor constante, conocido como la resistencia residual. Este valor depende no sólo del tipo de metal, sino en su pureza y su historia térmica. El valor de la resistencia residual de un metal es decidido por su concentración de impurezas. Algunos materiales pierden toda resistencia eléctrica a temperaturas suficientemente bajas, debido a un efecto conocido como superconductividad.
Una investigación de la resistencia de la baja temperatura de metales fue la motivación para De Heike Kamerlingh Onnes experimentos que condujeron en 1911 descubrimiento de superconductividad. Para más detalles consulte Historia de la superconductividad.
Semiconductores
En general, resistividad de semiconductores intrínsecos disminuye con el aumento de temperatura. Los electrones se golpeó a la banda de conducción energética por energía térmica, donde fluyen libremente y, al hacerlo así que deja detrás agujeros En banda de Valencia también que fluyen libremente. La resistencia eléctrica de un típico intrínseca (no dopado) semiconductor disminuye exponencial con la temperatura:
Una mejor aproximación de la dependencia de la temperatura de la resistencia de un semiconductor está dada por la Ecuación de Steinhart-Hart:
donde A, B y C son los llamados Coeficientes de Steinhart-Hart.
Esta ecuación se utiliza para calibrar termistores.
Semiconductores extrínsecos (dopados) tiene un perfil de temperatura mucho más complicado. A medida que aumenta la temperatura a partir de cero absoluto primero disminuyen abruptamente en resistencia como los portadores de los donantes o aceptadores. Después de que la mayoría de los donantes o aceptadores ha perdido sus portadores la resistencia comienza a aumentar otra vez ligeramente debido a la reducción movilidad de portadores (tanto como en un metal). En temperaturas más altas se comportará como semiconductores intrínsecos como los portadores de los donantes/aceptadores convierten insignificantes compararon con los portadores generados térmicamente.[38]
En semiconductores no cristalino, conducción puede ocurrir por cargos un túnel cuántico desde un sitio localizado a otro. Esto se conoce como margen variable saltando y tiene la forma característica de
-
 ,
,
donde n = 2, 3, 4, dependiendo de la dimensionalidad del sistema.
Conductividad y resistividad compleja
Al analizar la respuesta de los materiales a alternarse campos eléctricos (Espectroscopía Dieléctrica), en aplicaciones tales como tomografía de impedancia eléctrica,[39] es necesario sustituir la resistencia con un complejo cantidad llamada impeditivity (en analogía a Impedancia eléctrica). Impeditivity es la suma de un componente real, la resistividad y un componente imaginario, el reactividad (en analogía a reactancia). La magnitud de impeditivity es la raíz cuadrada de la suma de cuadrados de magnitudes de resistividad y reactividad.
Por el contrario, en tales casos la conductividad debe expresarse como una número complejo (o incluso como una matriz de números complejos, en el caso de anisotrópico materiales) llaman el admittivity. Admittivity es la suma de un componente real llamado la conductividad y un componente imaginario llamado la susceptibilidad.
Una descripción alternativa de la respuesta a las corrientes alternas utiliza una conductividad real (pero dependiente de la frecuencia), junto con un verdadero permitividad. La conductividad es el más grande, más rápido la señal de corriente alterna es absorbida por el material (es decir, más opaco el material es). Para obtener más información, vea Descripciones matemáticas de opacidad.
Ecuaciones del tensor para materiales anisótropos
Algunos materiales son anisotrópico, lo que significa que tienen diferentes propiedades en diferentes direcciones. Por ejemplo, un cristal de grafito Microscópicamente se compone de una pila de hojas y los flujos actuales muy fácilmente a través de cada hoja, pero se mueve mucho menos fácilmente de una hoja a otra.[28]
Para un material anisotrópico, no es generalmente válido para utilizar las ecuaciones escalares
Por ejemplo, la corriente no puede fluir en exactamente la misma dirección que el campo eléctrico. En cambio, se generalizan las ecuaciones a la forma del tensor 3D[40][41]
donde la conductividad σ y resistividad ρ rango-2 tensores (en otras palabras, 3 × 3 matrices). Las ecuaciones se ilustran compacto en forma de componente (usando notación del índice y el Convenio suma):[42]
El σ y ρ tensores son inversas (en el sentido de un matriz inversa). Los componentes individuales no son necesariamente inversos; por ejemplo, σxx No puede ser igual a 1 /ρxx.
Resistencia contra resistencia en geometrías complicadas
Si se conoce la resistividad del material, cálculo de la resistencia de algo de lo que puede, en algunos casos, ser mucho más complicado que la fórmula  por encima de. Un ejemplo es Perfiles de resistencia que se separa, donde el material es no homogénea (resistividad diferente en distintos lugares), y las rutas exactas del flujo actual no son obvias.
por encima de. Un ejemplo es Perfiles de resistencia que se separa, donde el material es no homogénea (resistividad diferente en distintos lugares), y las rutas exactas del flujo actual no son obvias.
En casos como éste, las fórmulas
necesitan ser reemplazados con
donde E y J Ahora campos vectoriales. Esta ecuación, junto con el ecuación de continuidad para J y el Ecuación de Poisson para E, forman un conjunto de ecuaciones diferenciales parciales. En casos especiales, una solución exacta o aproximada a estas ecuaciones puede ser trabajada a mano, pero para respuestas muy precisas en casos complejos, como métodos computacionales Análisis de elementos finitos puede ser necesario.
Productos de densidad de resistividad
En algunas aplicaciones donde el peso de un elemento es muy importante productos de resistividad densidad son más importantes que absoluta baja resistividad – es a menudo posible para que el conductor más grueso para compensar una resistencia más alta; y entonces es deseable un baja resistividad densidad producto material (o equivalente una conductancia alta cociente de densidad). Por ejemplo, para larga distancia líneas de alimentación aéreas, aluminio es frecuentemente usado en lugar de cobre porque es más ligero para la misma conductancia.
| Material | Resistividad (nΩ·m) | Densidad (g/cm3) | Resistividad densidad producto (nΩ·m·g/cm3) |
|---|---|---|---|
| Sodio | 47,7 | 0.97 | 46 |
| Litio | 92.8 | 0,53 | 49 |
| Calcio | 33.6 | 1.55 | 52 |
| Potasio | 72.0 | 0.89 | 64 |
| Berilio | 35,6 | 1.85 | 66 |
| Aluminio | 26,50 | 2,70 | 72 |
| Magnesio | 43.90 | 1.74 | 76.3 |
| Cobre | 16,78 | 8,96 | 150 |
| Plata | 15,87 | 10,49 | 166 |
| Oro | 22,14 | 19.30 | 427 |
| Hierro | 96.1 | 7.874 | 757 |
Plata, aunque es el metal menos resistente conocido, tiene una alta densidad y hace mal por esta medida. Calcio y los metales alcalinos tienen los mejores productos de resistividad densidad, pero rara vez se utilizan para los conductores debido a su alta reactividad con agua y oxígeno. El aluminio es mucho más estable. Dos otros atributos importantes, precio y toxicidad, excluyen la opción mejor (lo contrario): berilio. Así, el aluminio es generalmente el metal de elección cuando el peso de algunos requiere la conducción (o el costo de conducción) es el examen de conducción.
Véase también
- Conductividad cerca del umbral de percolación
- Resistencia de contacto
- Impedancia eléctrica
- Resistencias eléctricas de los elementos (página de datos)
- Tomografía de resistividad eléctrica
- La ley de Ohm
- Resistencia de la hoja
- Unidades del electromagnetismo
- Efecto de piel
Notas
- ^ Los números en esta columna aumentar o disminuir la mantisa porción de la resistividad. Por ejemplo, a 30 ° C (303 K), es la resistividad de plata 1.65×10−8. Esto se calcula como ΔΡ = Α ΔT Ρo donde ρo es la resistividad en 20 ° C (en este caso) y α es el coeficiente de temperatura.
- ^ Se denomina 100% IACS o estándar internacional de cobre recocido. La unidad para expresar la conductividad de los materiales no magnéticos por pruebas utilizando el por corrientes de Foucault método. Se utiliza generalmente para la verificación de temperamento y de la aleación de aluminio.
- ^ Oro es comúnmente usado en contactos eléctricos Porque no corroe fácilmente.
- ^ Comúnmente utilizado para líneas de alta tensión
- ^ 18% de cromo / 8% níquel acero inoxidable austenítico
- ^ Aleación de níquel-hierro-cromo comúnmente utilizada en elementos de calefacción.
- ^ El grafito es fuertemente anisotrópico.
- ^ a b La resistividad del semiconductores depende fuertemente de la presencia de impurezas en el material.
- ^ Corresponde a un promedio de salinidad de 35 g/kg en 20 ° C.
- ^ Este rango es típica de agua potable de alta calidad y no un indicador de calidad del agua
- ^ La conductividad es menor con monoatómico gases presentes; cambios en 1.2×10−4 desgasificación completa, o a 7.5×10−5 Tras equilibrar a la atmósfera debido a la disuelta CO2
Referencias
- ^ Lowrie. Fundamentos de Geofísica. Cambridge University Press. págs. 254 –. ISBN978-1-139-46595-3.
- ^ Narinder Kumar (2003). Integral física XII. Laxmi publicaciones. págs. 282 –. ISBN978-81-7008-592-8.
- ^ Eric Bogatin (2004). Integridad de la señal: simplificado. Prentice Hall profesional. págs. 114 –. ISBN978-0-13-066946-9.
- ^ Vinculación (sl). ibchem.com
- ^ "" Actual"frente a la velocidad de deriva. El aula de física. 20 de agosto de 2014.
- ^ Lowe, Doug (2012). Electrónica All-in-One para Dummies. John Wiley & Sons. ISBN978-0-470-14704-7.
- ^ "Resistencia eléctrica actual de electricidad - lección 3". El aula de física. 20 de agosto de 2014.
- ^ Suresh V Vettoor Superconductividad y la conducción eléctrica. Ias.AC.in. Septiembre de 2003
- ^ John C. Gallop (1990). CALAMARES, los efectos de Josephson y electrónica superconductora. CRC Press. págs. 3, 20. ISBN0-7503-0051-5.
- ^ D. los pinos (2002). "El modelo de fluctuación Spin para la superconductividad de alta temperatura: avances y perspectivas". La simetría de la brecha y las fluctuaciones en los superconductores de alta Tc. La OTAN ciencia serie: B: 371. Nueva York: Kluwer Academic. PP. 111-142. Doi:10.1007/0-306-47081-0_7. ISBN0-306-45934-5.
- ^ Ver Destellos en el cielo: ráfagas de rayos Gamma de la tierra provocados por un rayo
- ^ Eliezer Yafa, Shalom Eliezer, El cuarto estado de la materia: una introducción a la física del PlasmaEditor: Adam Hilger, 1989, ISBN 978-0-85274-164-1226 páginas, página 5
- ^ Bittencourt, J.A. (2004). Fundamentos de física de Plasma. Springer. p. 1. ISBN9780387209753.
- ^ Hong, Alicia (2000). "Rigidez dieléctrica del aire". El Factbook de la física.
- ^ Los físicos muestran los electrones pueden viajar más de 100 veces más rápido en el grafeno. Newsdesk.UMD.edu (2008-03-24). Recuperado encendido 2014-02-03.
- ^ a b c d e f g h i j k l m n o Raymond A. Serway (1998). Principios de la física (2ª ed.). Fort Worth, Texas; Londres: Saunders College Pub. p. 602. ISBN0-03-020457-7.
- ^ a b c David Griffiths (1999) [1981]. "7. electrodinámica". En Alison Reeves. Introducción a la electrodinámica (3ª ed.). Upper Saddle River, NJ: Prentice Hall. p. 286. ISBN0-13-805326-X. OCLC40251748.
- ^ Douglas Giancoli (2009) [1984]. 25. eléctricas corrientes y resistencia. En Jocelyn Phillips. Física para científicos e ingenieros con la física moderna (4ª ed.). Upper Saddle River, NJ: Prentice Hall. p. 658. ISBN0-13-149508-9.
- ^ Mesas de alambre de cobre: los Estados Unidos. La oficina nacional de estándares: gratis Descargar & Streaming: Internet Archive. Archive.org (2001-03-10). Recuperado encendido 2014-02-03.
- ^ Constantes físicas. (Formato PDF; Consulte la página 2, mesa en la esquina inferior derecha)]. Consultado el 17 / 12 / 2011.
- ^ Acero AISI 1010, frío dibujado. MatWeb
- ^ "Acero JFE" (PDF). 2012-10-20.
- ^ a b Douglas C. Giancoli (1995). Física: Principios con aplicaciones (4ª ed.). Londres: Prentice Hall. ISBN0-13-102153-2.
(véase también Tabla de resistividad. Hyperphysics.PHY-astr.gsu.edu) - ^ John o ' Malley (1992) Schaum de teoría y problemas de análisis de circuito básico, p. 19, McGraw-Hill Professional, ISBN 0-07-047824-4
- ^ Glenn Elert (Ed.), "La resistencia del acero", El Factbook de la física, obtenido y Programa archivado 16 de junio de 2011.
- ^ Milton Ohring (1995). Ciencia de materiales de ingeniería, volumen 1 (3ª ed.). Academic Press. p. 561. ISBN0125249950.
- ^ Y. Pauleau, Péter B. Barna, P. B. Barna (1997) Películas delgadas y recubrimientos protectores: síntesis, caracterización y aplicaciones, p. 215, Springer, ISBN 0-7923-4380-8.
- ^ a b Hugh O. Pierson, Manual de carbono, grafito, diamante y fullerenos: propiedades, procesamiento y aplicaciones, p. 61, William Andrew, 1993 ISBN 0-8155-1339-9.
- ^ Lawrence S. Pan, Don R. Kania, Diamante: propiedades electrónicas y aplicaciones, p. 140, Springer, 1994 ISBN 0-7923-9524-7.
- ^ Propiedades físicas del agua de mar. Kayelaby.NPL.co.uk. Recuperado encendido 2011-12-17.
- ^ a b c Datos de líneas de transmisión. Transmisión-line.net. Recuperado encendido 2014-02-03.
- ^ R. Pashley M., M. Rzechowicz, L. R. Pashley y M. J. Francis (2005). "Gas de agua es un agente de limpieza mejor". El Journal of Physical Chemistry B 109 (3): 1231 – 8. Doi:10.1021/jp045975a. PMID16851085.
- ^ S. D. Pawar, p. Murugavel, D. M. Lal (2009). "Efecto de la humedad relativa y el nivel del mar la presión sobre la conductividad eléctrica del aire sobre el océano Índico". Journal of Geophysical Research 114:: D02205. Bibcode:2009JGRD...11402205P. Doi:10.1029/2007JD009716.
- ^ Mesas de alambre de cobre. Dpto. de Estados Unidos de comercio. Oficina Nacional de normas manual. 21 de febrero de 1966
- ^ M.R. Ward (1971) Ciencias de la ingeniería eléctrica, págs. 36-40, McGraw-Hill.
- ^ A. Matthiessen, Rep Brit. Ass. 32, 144 (1862)
- ^ A. Matthiessen, Progg. Anallen, 122, 47 (1864)
- ^ Seymour J. (1972) Física electrónica, capítulo 2, Pitman
- ^ Otto H. Schmitt, Universidad de Minnesota Espectrometría de Impedivity mutua y la viabilidad de su incorporación al tejido de diagnóstico reconstrucción anatómica y multivariante medidas fisiológicas tiempo coherente. Otto-schmitt.org. Recuperado encendido 2011-12-17.
- ^ J.R. Tyldesley (1975) Una introducción al análisis tensorial: para ingenieros y científicos aplicadosLongman, ISBN 0-582-44355-5
- ^ G. Woan (2010) El manual de Cambridge de fórmulas de físicaCambridge University Press, ISBN 978-0-521-57507-2
- ^ K.F. Riley, M.P. Hobson, S.J. Bence (2010) Métodos matemáticos de la física e ingenieríaCambridge University Press, ISBN 978-0-521-86153-3
Lectura adicional
- Paul Tipler (2004). Física para científicos e ingenieros: electricidad, magnetismo, luz y la física moderna escuela primaria (5ª Ed.). W el. H. Freeman. ISBN0-7167-0810-8.
Enlaces externos
- "Conductividad eléctrica". Sesenta símbolos. Brady Haran para el Universidad de Nottingham. 2010.

 es el longitud de la pieza de material (medido en metrosm).
es el longitud de la pieza de material (medido en metrosm).
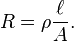



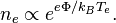

![\rho(T) = \rho_0[1+\alpha (T - T_0)]](http://upload.wikimedia.org/math/2/f/f/2ff526ba727868889bacc121855ed193.png)



 ,
,