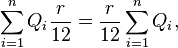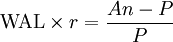Vida media ponderada

En Finanzas, la promedio ponderado de vida (WAL) de una amortización de préstamo o amortización de bonos, también llamado vida media, es el promedio ponderado de los tiempos de la reembolsos del principal: es el tiempo medio hasta un dólar de capital es reembolsado.

En una fórmula,

$\text{WAL} = \sum_{i=1}^n \frac {P_i}{P} t_i,$

donde:

• $P$ es el principal (total),
• $P_i$ es el pago principal que se incluye en el pago $i$, por lo tanto
• $\frac{P_i}{P}$ es la fracción del total que se incluye en el pago principal $i$, y
• $t_i$ es el tiempo (en años) desde la fecha de cálculo para el pago $i$.

Si lo desea, $t_i$ puede ser ampliado como $\frac{1}{12}(i+\alpha-1)$ para un bono mensual, donde $\alpha$ es la fracción de un mes entre fecha de liquidación y la primera fecha de flujo de efectivo.

WAL de las clases de préstamos

En préstamos que permiten pago por adelantado, el WAL no puede ser computado desde el esquema de amortización solo; uno también debe hacer suposiciones sobre el prepago y el comportamiento por defecto, y la citada WAL será una estimación. La WAL se calcula generalmente de una secuencia simple de flujo de efectivo. En ocasiones, un vida media simulada puede ser computado de escenarios de flujo de efectivo, como las de un ajustados a la opción de propagación modelo.

Conceptos relacionados

WAL no se debe confundir con los siguientes conceptos distintos:

Duración del bono

Duración del bono es el promedio ponderado en el tiempo para recibir el descuento valores actuales de todos los flujos de efectivo (incluyendo capital e intereses), mientras que WAL es el tiempo promedio ponderado para recibir simplemente los pagos de capital (intereses no incluidos y no descuento). Para un préstamo de amortización con pagos iguales, el WAL será mayor que la duración, como los primeros pagos se ponderan hacia interés, mientras que los pagos posteriores se ponderan hacia principal, y además, tomando el valor actual (en duración) descuentos de los pagos posteriores.

Hasta 50% del capital ha sido pagado

WAL es un significa, mientras que "el 50% del capital pagado" es un mediana; Ver diferencia entre media y mediana. Esto es un malentendido común. Puesto que es excepcional una función cóncava (de momento) para el plano pago amortización de préstamo, menos que media el director habrá sido pagado en la WAL. Intuitivamente, esto es porque pasa la mayor parte de la devolución principal al final. Formalmente, tiene la distribución de los reembolsos sesgo negativo: los reembolsos del principal pequeño al principio arrastra WAL (media) más reducen la mediana.

Madurez de promedio ponderado (WAM)

WAM es el promedio de la fechas de vencimiento de múltiples préstamos, no un promedio de reembolsos del principal.

Aplicaciones

WAL es una medida que puede ser útil en el análisis de riesgo de crédito en títulos de renta fija, teniendo en cuenta que el riesgo principal de un préstamo es el riesgo de pérdida del principal. Todo lo demás igual, un bono con director excepcional ya (es decir, más tiempo WAL) tiene mayor riesgo de crédito de un bono con menor WAL. En particular, WAL es de uso frecuente como base para las comparaciones del rendimiento en Propagación cálculos.

WAL no puede usarse para estimar la sensibilidad precio de los bonos a fluctuaciones de tasas de interés, como WAL incluye solamente los principales flujos de efectivo, omitiendo el pago de intereses. En cambio, uno debe utilizar duración del bono, que incorpora todos los flujos de efectivo.

Ejemplos

WAL de un préstamo de bala (no amortizado) es exactamente el tenor, el principal es pagado precisamente a la madurez.

En un préstamo de amortización de 30 años, pagando cantidades iguales cada mes, uno tiene las siguientes WALs, de las tasas de interés anuales determinadas (y correspondientes pagos mensuales por el saldo de $100.000, calculado a través de un Calculadora de amortización y las fórmulas a continuación relativos amortizan los pagos, el interés total y WAL):

Tasa de	Pago	Interés total	Cálculo de WAL	WAL
4%	$477,42	$71.871,20	$71,871.20/($100,000*4%)	17.97
8%	$733,76	$164,153.60	$164,153.60/($100,000*8%)	20.52
12%	$1.028,61	$270,299.60	$270,229.60/($100,000*12%)	22,52

Tenga en cuenta que a medida que aumenta la tasa de interés, WAL aumenta, puesto que los pagos principales se convierten cada vez más cargado de espalda. WAL es independiente del saldo del principal, aunque total interés y los pagos son proporcionales al Director.

Para un cupón de 0%, donde el principal se amortiza linealmente, la WAL es exactamente mitad el tenor más media un período de pago, porque el principal es pagado en mora (en el final de la época). Así que para un préstamo a 30 años de 0%, pagar mensualmente, el WAL $15 + 1/24 \approx 15.04$ años.

Interés total

WAL permite calcular fácilmente los pagos de interés total, dado por:

$\text{WAL} \times r \times P,$

donde r es la tasa de interés anual y P es el principal inicial.

Esto puede entenderse intuitivamente como: "el medio dólar de principal destaca por la WAL, por lo tanto es el interés en el dólar promedio 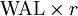$\text{WAL} \times r$y ahora uno se multiplica por el principal para obtener los pagos de intereses total. "

A prueba de

Más rigurosamente, uno puede derivar el resultado siguiente. Para facilitar la exposición, asume que los pagos son mensuales, así que periódicamente la tasa de interés es la tasa de interés anual dividido por 12 y el tiempo $t_i = i/12$ (tiempo en años es número de período en más de 12 meses).

A continuación:

$\begin{align} \text{WAL} &= \sum_{i=1}^n \frac {P_i}{P} t_i\\ \text{WAL} \times P &= \sum_{i=1}^n P_i t_i &&= \sum_{i=1}^n P_i \frac{i}{12}\\ \text{WAL} \times P \times r &= \sum_{i=1}^n iP_i \frac{r}{12} &&= \frac{r}{12} \sum_{i=1}^n iP_i \end{align}$

Interés total es

$\sum_{i=1}^n Q_i \frac{r}{12} = \frac{r}{12}\sum_{i=1}^n Q_i,$

donde $Q_i$ es el principal en la Inicio del período de i (es el principal en la que el i pago de intereses se basa). La declaración se reduce a demostrar $\sum_{i=1}^n iP_i=\sum_{i=1}^n Q_i$. Estas cantidades son el principal total ponderado en el tiempo del bono (en períodos), y son simplemente diferentes maneras de cortarlo: el $iP_i$ cuentas en definitiva cómo largo cada dólar de principal es excepcional (corta horizontalmente), mientras que el $Q_i$ cuenta cuánto es excepcional en cada momento (corta verticalmente).

Trabajando hacia atrás, 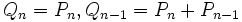$Q_n=P_n, Q_{n-1}=P_n+P_{n-1}$, y así sucesivamente: el principal excepcional cuando k permanecen períodos es exactamente la suma de la siguiente k pagos de capital. El principal pagado por el último (npago principal del TH) es excepcional para todos n períodos, mientras que el principal pagado por el segundo al último ()n− 1) th) es excepcional para pago principal n− 1 periodos y así sucesivamente. Con esto, las sumas se pueden organizar vuelva a ser igual.

Por ejemplo, si el principal amortizado como $100, $80, $50 (con paydowns de $20, $30, $50), luego la suma por un lado sería 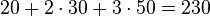$20+2\cdot 30 + 3\cdot 50=230$y por otro lado sería $100+80+50=230$. Esto se demuestra en la siguiente tabla, que muestra el esquema de amortización, en reembolsos del principal, donde cada columna es un $Q_i$, y cada fila es $iP_i$:

230	100	80	50
1 × 20	20
2 × 30	30	30
3 × 50	50	50	50

Informática WAL de pago amortizado

Lo anterior se puede invertir: dadas las condiciones (principal, tenor, tarifa) y pago amortizado A, uno puede computar el WAL sin saber el plan de amortización. Los pagos totales son $An$ y los pagos de intereses totales son $An-P$, por lo que es el WAL:

$\text{WAL} = \frac{An-P}{Pr}$

Del mismo modo, el interés total como porcentaje del capital está dado por 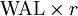$\text{WAL} \times r$:

$\text{WAL} \times r = \frac{An-P}{P}$

Notas y referencias

• Fabozzi, Frank J. (2000), El manual de títulos de renta fija, ISBN0-87094-985-3

Véase también

• Calculadora de amortización
• Plan de amortización
• Amortización de préstamo

Otras Páginas

• IBM ThinkPad ThinkLight
• Posiciones quirurgicas
• Chris Kyle
• Encanto de blackBerry
• Dinero divertido (desambiguacion)
• Touch n Go (contadores de efectivo de seccion)
• Java (banda)
• Dinis Alves