Tiempo de generación

En Biología de poblaciones y Demografía, la tiempo de generación es el promedio tiempo entre dos generaciones consecutivas en los linajes de un población. En las poblaciones humanas, la generación normalmente oscila entre 20 y 30 años. Historiadores a veces utilizan esto para eventos fecha, convirtiendo las generaciones en años para obtener estimaciones aproximadas de tiempo.

Definiciones y fórmulas correspondientes

Las definiciones existentes del tiempo de generación se dividen en dos categorías: los que tratan el tiempo de generación como un tiempo de renovación de la población y los que se centran en la distancia entre los individuos de una generación y la siguiente. A continuación se muestran que los tres más comúnmente utilizados definiciones:

• El tiempo que tarda la población a crecer por un factor de su tasa reproductiva neta:

La tasa neta de reproducción $\textstyle R_0$ es el número de crías que un individuo se espera que produzca durante toda su vida (una tasa reproductiva neta de 1 significa que la población se encuentra en su equilibrio demográfico). Esta definición contempla el tiempo de generación como un tiempo de renovación de la población. Justifica la definición muy simple utilizada en Microbiología ("el tiempo que tarda para que la población doble", o tiempo de duplicación) ya que se puede considerar que durante la fase exponencial del crecimiento bacteriano la mortalidad es muy baja y como resultado un bacteria se espera que ser sustituido por dos bacterias en la generación siguiente (la célula madre y la hija de la célula). 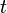Si la dinámica de población es exponencial con una tasa de crecimiento $\textstyle r$ (es decir$\textstyle n(t) \propto \exp(rt)$, donde $\textstyle n(t)$ es el tamaño de la población en el tiempo $\textstyle t$), entonces esta medida del tiempo de generación viene dada por:

$T = \frac{\log R_0}{r}$.

De hecho, 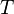$\textstyle T$ es tal que $\textstyle n(t + T) = R_0 \, n(t)$, es decir, $\textstyle \exp(rT) = R_0$.

• La diferencia promedio de edad entre padres e hijos cuando la población se encuentra en la distribución de edad estable:

Esta definición es una medida de la distancia entre las generaciones en lugar de un momento de renovación de la población. Puesto que muchos modelos demográficos están basados en la mujer (es decir, que sólo tienen las hembras en cuenta), esta definición a menudo se expresa como una distancia de madre e hija (la "edad media de las madres en el nacimiento de sus hijas"). Sin embargo, también es posible definir una distancia de padre e hijo (edad media de los padres a la edad de sus hijos) o no a tener sexo en cuenta en la definición. En los modelos de estructura de la edad de la población, una expresión viene dada por:

$T = \int_0^{\infty} x e^{-rx} l(x) m(x) \, \mathrm{d}x$,

donde $\textstyle r$ es la tasa de crecimiento de la población, $\textstyle l(x)$ es la función de supervivencia (probabilidad de que una persona sobrevive a la edad $\textstyle x$) y $\textstyle m(x)$ la función de maternidad (o función de nacimiento o fecundidad específicas por edad). Para modelos de población matriz, hay una fórmula más simple y general:

$T = \frac{ \lambda v w }{v F w} = \frac{1}{\sum e_{\lambda} ( f_{ij} )}$,

donde $\textstyle \lambda = e^r$ es la tasa de tiempo discreto crecimiento de la población, $\textstyle F = (f_{ij})$ es la matriz de su fertilidad, $\textstyle v$ su valor reproductivo (vector fila) y $\textstyle w$ su distribución etapa estable (vector columna); el $\textstyle e_{\lambda}(f_{ij}) = \frac{f_{ij}}{\lambda} \frac{\partial \lambda}{\partial f_{ij}}$ son la elasticidades de $\textstyle \lambda$ 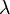a las fertilidades.

• La edad en que los miembros de una determinada cohorte se esperan para reproducir:

Esta definición es muy similar a la anterior, pero la población no tiene que ser en su distribución por edad estable. Además, puede ser computado para diferentes cohortes y así proporcionar más información sobre el tiempo de generación en la población. Esta medida viene dada por:

$T = \frac{\int_{x=0}^{\infty} x l(x) m(x) }{\int_{x=0}^{\infty} l(x) m(x) }$.

De hecho, el numerador es la suma de las edades en el cual se reproduce un miembro de la cohorte y el denominador es $\textstyle R_0$, el número promedio de hijos que produce.

Otras Páginas

• Bart Goor
• IBM (redireccion de International Business Machines Corporation)
• Collar (animal)
• Halliburton (categoria empresas con sede en Houston)