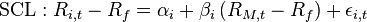Teoría moderna de portafolio
Teoría moderna de portafolio (MPT) es una teoría de Finanzas que intenta maximizar la cartera esperada retorno para una cantidad dada de riesgo de la cartera, o minimizar el equivalente riesgo para un determinado nivel de rentabilidad esperada, eligiendo cuidadosamente las proporciones de varios activos. Aunque MPT es ampliamente utilizado en la práctica en la industria financiera y varios de su creadores ganó un Premio Nobel para la teoría,[1] en los últimos años las asunciones básicas del MPT han sido ampliamente cuestionadas por los campos tales como economía conductista.
MPT es una formulación matemática del concepto de diversificación en invertir, con el fin de seleccionar una colección de inversión activos que tiene colectivamente menor riesgo que cualquier activo individual. Esto es posible, intuitivamente hablando, porque diferentes tipos de activos a menudo cambian de valor en sentidos opuestos.[2] Por ejemplo, a los precios de grado en la mercado de valores mover diferentemente de los precios en el mercado de bonos, una colección de ambos tipos de activos puede en cara teoría disminuir riesgo global que individualmente. Pero la diversificación disminuye riesgo aunque los rendimientos de los activos no se correlacionan negativamente — de hecho, incluso si se correlacionan positivamente.[3]
Técnicamente, MPT modelos más activo el retorno como un distribuye normalmente función (o más generalmente como una elíptico distribuidos variable aleatoria), define riesgo como el desviación estándar de regreso y modelos de una cartera como una combinación ponderada de activos, para que el retorno de un portafolio es la combinación de los activos ponderada devuelve. Mediante la combinación de diferentes activos cuyos rendimientos no están perfectamente positivamente correlacionadosMPT encaminada a reducir el total varianza de la cartera de retorno. MPT también asume que los inversionistas están racional y los mercados son eficiente.
MPT fue desarrollado en la década de 1950 a través de la década de 1970 y fue considerado un avance importante en la modelación matemática de las finanzas. Desde entonces, algunos teóricos y prácticos críticas que se nivelaron contra él. Estos incluyen pruebas que rendimientos financieros no siguen un Distribución Gausiana o de hecho cualquier distribución simétrica y las correlaciones entre las clases de activos no son fijos, pero pueden variar dependiendo de eventos externos (especialmente en las crisis). Además, existe evidencia de que los inversionistas no son racional y los mercados no pueden ser eficiente.[4][5] Finalmente, en conflicto con la anomalía de baja volatilidad CAPMde Asunción compensación de riesgo más alto de rendimiento más alta. Afirma que una cartera consiste en acciones de baja volatilidad (como blue chip existencias) cosecha mayores retornos ajustados por riesgo de una cartera con acciones de alta volatilidad (como ilíquidos penny stocks). Un estudio realizado por Myron Scholes, Michael Jensen, y Fischer Black en 1972 sugiere que la relación entre retorno y Beta puede ser plana o incluso negativamente correlacionados.[6]
Contenido
- 1 Concepto
- 2 Historia
- 3 Modelo matemático
- 3.1 Riesgo y rentabilidad esperada
- 3.2 Diversificación
- 3.3 La frontera eficiente con ningún activo libre de riesgo
- 3.4 Teorema de dos fondos de inversión
- 3.5 El activo libre de riesgo y la línea de asignación de capital
- 4 Asset pricing usando MPT
- 4.1 Riesgo sistemático y riesgo específico
- 4.2 Modelo de precios de activos de capital
- 5 Críticas
- 5.1 Supuestos
- 5.2 MPT no modelo realmente el mercado
- 5.3 El MPT no tener en cuenta su propio efecto sobre los precios de los activos
- 6 Extensiones
- 7 Otras aplicaciones
- 7.1 Aplicaciones en carpetas de proyecto y otros activos "no financieros"
- 7.2 Aplicación a otras disciplinas
- 8 Comparación con arbitraje de precios teoría
- 9 Véase también
- 10 Referencias
- 11 Lectura adicional
- 12 Enlaces externos
Concepto
El concepto fundamental detrás de MPT es el activos en una inversión cartera No debe ser seleccionado individualmente, cada uno por sus propios méritos. Por el contrario, es importante considerar cómo cada activo cambios en el precio en relación a cómo todos los otros activos en la cartera de cambios en el precio.
La inversión es un equilibrio entre riesgo y se espera retorno. En general, los activos con mayores rendimientos esperados son más riesgosos. Las poblaciones en una cartera eficiente es elegido según tolerancia al riesgo del inversionista, una cartera eficiente se dice tener una combinación de al menos dos poblaciones por encima de la cartera de varianza mínima. Para una cantidad dada de riesgo, MPT describe cómo seleccionar una cartera con la más alta rentabilidad esperada posible. O, para un determinado retorno esperado, MPT explica cómo seleccionar una cartera con el menor riesgo posible (el retorno esperado objetivo no puede ser más que la de retorno más alta seguridad disponible, por supuesto, menos negativas tenencias de activos son posibles.)[7]
Por lo tanto, MPT es una forma de diversificación. Bajo ciertas supuestos y específicos cuantitativa definiciones de riesgo y retorno, MPT explica cómo encontrar la mejor estrategia posible diversificación.
Historia
Harry Markowitz en un artículo de 1952 introdujo MPT[8] y un libro de 1959.[9] Markowitz clasifica simplemente como "Teoría del portafolio" porque "No hay nada moderno en ello". Véase también esto[7] estudio de la historia.
Modelo matemático
En cierto sentido la derivación matemática abajo es MPT, aunque los conceptos básicos del modelo también han sido muy influyentes.[7]
En esta sección se desarrolla el modelo "clásico" de MPT. Ha habido muchos extensiones desde.
Riesgo y rentabilidad esperada
MPT asume que los inversionistas son reacios al riesgo, lo que significa que dado dos carteras que ofrecen los mismos inversores esperados retorno, preferirá el que menos riesgoso. Así, un inversionista tendrá el mayor riesgo sólo si compensado por mayores rendimientos esperados. Por el contrario, un inversionista que quiere mayor espera devoluciones deben aceptar más riesgo. La compensación exacta será el mismo para todos los inversores, pero diversos inversionistas evaluará las ventajas y desventajas diferente basada en las características de aversión al riesgo individual. La implicación es que un racional inversionista no invertirá en una cartera si existe una segunda cartera con una más favorable Perfil de retorno esperado riesgo – es decir, si para ese nivel de riesgo de una cartera de alternativa existe que mejor se espera retornos.
Tenga en cuenta que la teoría utiliza la desviación estándar del retorno como un proxy por riesgo, lo cual es válido si los retornos de activos son distribuye normalmente conjuntamente o de otro tipo elíptico distribuidos. Hay problemas con esto, sin embargo; ver crítica.
Bajo el modelo:
- Cartera de retorno es la combinación de proporción ponderada de los retornos de los constituyentes activos.
- La volatilidad de la cartera es una función de la correlaciones ρij de los activos del componente, para todos (pares) activoi, j).
En general:
- Rentabilidad esperada:

- donde
es el retorno de la cartera,
es el retorno sobre activos i y
es la ponderación del componente activo
(es decir, la proporción del activo "i" de la cartera).
- Varianza retorno de portafolio:
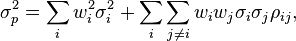
- donde
es el coeficiente de correlación entre los rendimientos de los activos i y j. Alternativamente la expresión puede ser escrita como:
,
- donde
para i= j.
- Cartera de retorno volatilidad (desviación estándar):

Para un dos activos Portfolio:
- Cartera de retorno:
- Varianza del portafolio:
Para un tres activos Portfolio:
- Cartera de retorno:
- Varianza del portafolio:
Diversificación
Un inversionista puede reducir riesgo de cartera manteniendo las combinaciones de instrumentos que no están perfectamente positivamente correlacionados (coeficiente de correlación  ). En otras palabras, los inversionistas pueden reducir su exposición al riesgo activo individual mediante la celebración de un diversificado cartera de activos. La diversificación puede permitir la misma cartera esperada retorno con un menor riesgo. Estas ideas han sido iniciadas con Markowitz y luego reforzado por otros economistas y matemáticos tales como Andrew Brennan que han expresado ideas en la limitación de la varianza a través de la teoría de cartera.
). En otras palabras, los inversionistas pueden reducir su exposición al riesgo activo individual mediante la celebración de un diversificado cartera de activos. La diversificación puede permitir la misma cartera esperada retorno con un menor riesgo. Estas ideas han sido iniciadas con Markowitz y luego reforzado por otros economistas y matemáticos tales como Andrew Brennan que han expresado ideas en la limitación de la varianza a través de la teoría de cartera.
Si todos los pares de activos tienen correlaciones de 0 — están perfectamente correlacionados — varianza retorno de la cartera es la suma sobre todos los activos de la Plaza de la fracción en el activo veces varianza retorno del activo (y la desviación estándar de la cartera es la raíz cuadrada de esta suma).
La frontera eficiente con ningún activo libre de riesgo
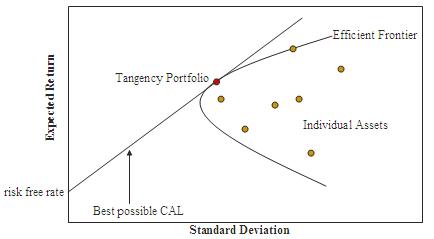
Como se muestra en este gráfico, cada combinación posible de los activos riesgosos, sin incluir ningún existencias del activo libre de riesgo, se puede trazar en riesgo esperado retorno espacio, y la colección de todas esas carteras posibles define una región en este espacio. El límite izquierdo de esta región es una hipérbola,[10] y el borde superior de esta región es la frontera eficiente en la ausencia de un activo libre de riesgo (a veces llamado "the bullet Markowitz"). Combinaciones a lo largo de este borde superior representan carteras (no incluyendo existencias del activo libre de riesgo) para que existe el riesgo más bajo para un determinado nivel de rentabilidad esperada. Equivalente, una cartera tirada en la frontera eficiente representa la oferta de combinación el retorno esperado mejor posible para dado el nivel de riesgo.
Matrices son preferidas para los cálculos de la frontera eficiente.
En forma de matriz, para una dada "la tolerancia del riesgo"
, se encuentra la frontera eficiente reduciendo al mínimo la siguiente expresión:

donde
es un vector de pesos de cartera y
(Los pesos pueden ser negativos, lo que significa que los inversores pueden corto seguridad.);
es el matriz de covarianza para los rendimientos de los activos de la cartera;
es un factor "riesgo de tolerancia", donde 0 resultados en la cartera con riesgo mínimo y
resultados de la cartera infinitamente lejos de la frontera con rentabilidad esperada y riesgo sin límites; y
es un vector de retornos esperados.
es la varianza de la cartera de retorno.
es el retorno esperado de la cartera.
La optimización de arriba encuentra el punto de la frontera en la que sería la inversa de la pendiente de la frontera q Si cartera devuelve la varianza en lugar de desviación estándar se trazaron horizontalmente. La frontera en su totalidad es paramétrica en q.
Muchos paquetes de software, incluyendo MATLAB, Microsoft Excel, Mathematica y R, proporcionar optimización rutinas adecuadas para el problema anterior.
Un enfoque alternativo para especificar la frontera eficiente es tan forma paramétrica de la cartera que se espera devolver
Esta versión del problema requiere que minimizamos
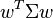
sujeto a

para el parámetro
. Este problema se soluciona fácilmente usando un Multiplicadores de Lagrange.
Teorema de dos fondos de inversión
Un resultado clave del análisis anterior es el Teorema de dos fondos de inversión.[10] Este teorema establece que cualquier cartera en la frontera eficiente puede ser generado mediante la celebración de una combinación de cualquier dos carteras dadas en la frontera; las carteras dadas dos últimas son los "fondos mutuos" en nombre del teorema. Así que en la ausencia de un activo libre de riesgo, un inversionista puede lograr deseados cartera eficiente incluso si todo lo que es accesible es un par de fondos de inversión eficientes. Si la situación de la cartera deseada en la frontera entre las ubicaciones de los dos fondos de inversión, los fondos mutuos se celebrará en cantidades positivas. Si la cartera deseada está fuera del intervalo atravesado por los dos fondos de inversión, entonces uno de los fondos mutuos debe ser vendido corto (celebrado en cantidad negativa) mientras que el tamaño de la inversión en otro fondo mutuo debe ser mayor que la cantidad disponible para la inversión (el exceso siendo financiado por el préstamo del fondo de otro).
El activo libre de riesgo y la línea de asignación de capital
El activo libre de riesgo es el activo (hipotético) que paga un tasa libre de riesgo. En la práctica, valores gubernamentales a corto plazo (como Estados Unidos Letras del tesoro) se utilizan como un activo libre de riesgo, porque pagan una tasa fija de interés y tienen excepcionalmente bajo por defecto riesgo. El activo libre de riesgo tiene cero variación en los rendimientos (por lo tanto es libre de riesgo); es también no correlacionado con cualquier otro activo (por definición, puesto que su varianza es cero). Como resultado, cuando se combina con cualquier otro activo o portafolio de activos, el cambio a cambio está linealmente relacionado con el cambio en riesgo ya que varían las proporciones en la combinación.
Cuando se introduce un activo libre de riesgo, la half-line que se muestra en la figura es la nueva frontera eficiente. Es tangente a la hipérbola en la cartera de riesgosa pura con el más alto Ratio de Sharpe. Su intercepción vertical representa una cartera con 100% de las explotaciones en el activo libre de riesgo; la tangencia con la hipérbola representa una cartera sin explotaciones libres de riesgo y el 100% de activos de la cartera que ocurre en el punto de tangencia; entre esos puntos son carpetas que contienen cantidades positivas de la cartera de tangencia arriesgado tanto el activo libre de riesgo; y son los puntos en el half-line más allá del punto de tangencia apalancadas carpetas de explotaciones negativas del activo libre de riesgo (este último se ha vendido corto — en otras palabras, el inversionista ha prestado a la tasa libre de riesgo) y un monto invertido en la cartera de tangencia equivalente a más del 100% del capital inicial del inversionista. Este eficiente half-line se llama el línea de asignación de capital (CAL), y su fórmula puede ser demostrado ser
En esta fórmula P es el portafolio de activos riesgosos en la tangencia con la bala de Markowitz, sub F es el activo libre de riesgo, y C es una combinación de carteras P y F.
Por el diagrama, la introducción del activo libre de riesgo como un posible componente de la cartera ha mejorado el rango de riesgo esperado retorno combinaciones disponibles, porque en todas partes excepto en la cartera de tangencia el half-line le da una mayor rentabilidad esperada de la hipérbola hacen a todos los niveles de riesgo posible. El hecho de que todos los puntos en el locus eficiente lineal pueden lograrse mediante una combinación de existencias del activo libre de riesgo y la cartera de tangencia es conocida como el Teorema de un fondo mutuo,[10] donde el fondo mutuo que se refiere es la cartera de tangencia.
Asset pricing usando MPT
El análisis anterior describe el comportamiento óptimo de un inversionista individual. Asset pricing teoría se basa en este análisis de la siguiente manera. Dado que todo el mundo tiene los activos riesgosos en idénticas proporciones uno al otro — es decir en las proporciones dadas la cartera de tangencia — en equilibrio de mercado los precios de los activos riesgosos y por lo tanto sus ganancias esperadas, se ajustan para que las proporciones de la cartera de tangencia son las mismas que las proporciones en que los activos riesgosos son suministrados al mercado. Por lo tanto relativas suministros serán igual a demandas relativas. MPT deriva la necesaria rentabilidad esperada para un activo correctamente tasado en este contexto.
Riesgo sistemático y riesgo específico
Riesgo específico es el riesgo asociado con los activos individuales - dentro de una cartera de estos riesgos pueden reducirse mediante la diversificación (riesgos específicos "Cancelar hacia fuera"). Riesgo específico también se llama riesgo diversificables, único, asistemático o idiosincrásico. Riesgo sistemático (también conocido como riesgo de cartera o riesgo de mercado) se refiere al riesgo común a todos los valores — excepto por venta corta como se indica más abajo, no se puede diversificar riesgo sistemático lejos (dentro de un mercado). Dentro de la cartera de mercado, riesgos específicos del activo se diversificará lejos a la medida de lo posible. Riesgo sistemático, por tanto, se compara con el riesgo (desviación estándar) de la cartera de mercado.
Puesto que se comprará una seguridad sólo si mejora las características de retorno esperado riesgo de la cartera de mercado, la medida relevante del riesgo de seguridad es el riesgo que se añade a la cartera de mercado y no su riesgo en aislamiento. En este contexto, la volatilidad de los activos y su correlación con la cartera de mercado, se observan históricamente y por lo tanto reciben. (Existen varios enfoques para activos precios ese intento de activos precio por modelar las propiedades estocásticas de los momentos de los retornos de activos - estos se conocen ampliamente como activo condicional precios modelos.)
Los riesgos sistemáticos dentro de un mercado pueden gestionarse a través de una estrategia de posiciones de corto y largo dentro de una cartera, creando una cartera "neutral del mercado". Carteras neutrales del mercado, por lo tanto tendrá una correlación de cero.
Modelo de precios de activos de capital
El retorno activo depende de la cantidad pagada por el activo hoy. El precio pagado debe asegurarse de que la cartera de mercado de riesgo / retorno características mejoran cuando el activo se agrega a ello. El CAPM es un modelo que se deriva la teórica necesaria rentabilidad esperada (es decir, tasa de descuento) para un activo en un mercado, dada la tasa libre de riesgo disponible a los inversionistas y el riesgo del mercado en su conjunto. El CAPM se expresa generalmente:
 Beta, es la medida de la sensibilidad de activos a un movimiento en el mercado en general; Beta se encuentra generalmente vía regresión en los datos históricos. Betas superior a uno significan contribución promedio más de "riesgo" en el sentido de los activos riesgo de la cartera total; betas debajo de uno indican un más bajo que la contribución de riesgo medio.
Beta, es la medida de la sensibilidad de activos a un movimiento en el mercado en general; Beta se encuentra generalmente vía regresión en los datos históricos. Betas superior a uno significan contribución promedio más de "riesgo" en el sentido de los activos riesgo de la cartera total; betas debajo de uno indican un más bajo que la contribución de riesgo medio.
 es la prima de mercado, la rentabilidad esperada de excesiva de la cartera mercado espera regresar sobre la tasa libre de riesgo.
es la prima de mercado, la rentabilidad esperada de excesiva de la cartera mercado espera regresar sobre la tasa libre de riesgo.
La derivación es como sigue:
(1) el impacto incremental en riesgo y rentabilidad esperada cuando un activo riesgoso adicional, a, se añade a la cartera de mercado, m, se desprende de las fórmulas para una cartera de dos activos. Estos resultados se utilizan para obtener la tasa de descuento apropiada activos.
- Riesgos de la cartera de mercado =
- Por lo tanto, riesgo añadido a la cartera =
![[ w_a^2 \sigma_a^2 + 2 w_m w_a \rho_{am} \sigma_a \sigma_m]](//upload.wikimedia.org/math/0/6/5/065759bd620995bdd1a7653abf3f9047.png)
- Pero dado que el peso de los activos será relativamente bajo,
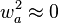
- es decir, riesgo adicional =
![[ 2 w_m w_a \rho_{am} \sigma_a \sigma_m] \quad](//upload.wikimedia.org/math/5/b/1/5b146f9f3dfe9825bef30e7fbb900c64.png)
- Retorno esperado del portafolio de mercado =
- Por lo tanto adicional esperado regreso =
![[ w_a \operatorname{E}(R_a) ]](//upload.wikimedia.org/math/2/9/2/292f0f3fd92a3bdf1fa91cc492cecda0.png)
(2) si un activo, a, está tasado correctamente, la mejora en su cociente retorno espera riesgo alcanzada agregándolo a la cartera de mercado, m, por lo menos coincidirá con las ganancias de gastar ese dinero en un creciente interés en la cartera de mercado. La suposición es que el inversionista comprará los activos con fondos prestados a la tasa libre de riesgo,
; Esto es racional si
.
- Por lo tanto:
![[ w_a ( \operatorname{E}(R_a) - R_f ) ] / [2 w_m w_a \rho_{am} \sigma_a \sigma_m] = [ w_a ( \operatorname{E}(R_m) - R_f ) ] / [2 w_m w_a \sigma_m \sigma_m ]](//upload.wikimedia.org/math/e/8/d/e8db53a1d6ccf7f92d3172ca2d6513c9.png)
- es decir:
![[\operatorname{E}(R_a) ] = R_f + [\operatorname{E}(R_m) - R_f] * [ \rho_{am} \sigma_a \sigma_m] / [ \sigma_m \sigma_m ]](//upload.wikimedia.org/math/c/f/d/cfdeeddd7d3731cb61a106fbe18a9766.png)
- es decir:
![[\operatorname{E}(R_a) ] = R_f + [\operatorname{E}(R_m) - R_f] * [\sigma_{am}] / [ \sigma_{mm}]](//upload.wikimedia.org/math/b/3/b/b3b928bc81cc747286a4008802276277.png)
es la "beta",
retorno — la covarianza entre el retorno del activo y el mercado de retorno dividido por la variación de la rentabilidad de mercado — es decir, la sensibilidad del precio del activo al movimiento en el valor de la cartera de mercado.
Esta ecuación puede ser Estimado estadísticamente utilizando la siguiente regresión ecuación:
donde αi se llama del activo Alfa, Βi es el activo coeficiente beta y SCL es el línea característica de seguridad.
Una vez el retorno esperado de un activo, 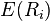 , se calcula utilizando el CAPM, el futuro flujos de efectivo del activo puede ser con descuento a sus valor actual usando esta tasa para establecer el precio correcto para el activo. Una acción más riesgosa tendrá un beta más alto y será descontada a una tasa más alta; existencias menos sensibles tendrán menores betas y descontadas a una tasa más baja. En teoría, un activo es precio correctamente cuando su precio observado es la misma que su valor calculado utilizando el CAPM derivados de tasa de descuento. Si el precio observado es superior a la valoración, el activo está sobrevaluado; está subvaluado por un precio muy bajo.
, se calcula utilizando el CAPM, el futuro flujos de efectivo del activo puede ser con descuento a sus valor actual usando esta tasa para establecer el precio correcto para el activo. Una acción más riesgosa tendrá un beta más alto y será descontada a una tasa más alta; existencias menos sensibles tendrán menores betas y descontadas a una tasa más baja. En teoría, un activo es precio correctamente cuando su precio observado es la misma que su valor calculado utilizando el CAPM derivados de tasa de descuento. Si el precio observado es superior a la valoración, el activo está sobrevaluado; está subvaluado por un precio muy bajo.
Críticas
A pesar de su importancia teórica, críticos del MPT preguntan si es una estrategia de inversión ideal, porque su modelo de los mercados financieros no coincide con el mundo real de muchas maneras.[11]
Los esfuerzos para traducir la fundamentación teórica a un algoritmo de construcción viable cartera han estado plagados de dificultades técnicas derivadas de la inestabilidad de la original problema de optimización con respecto a los datos disponibles. Investigaciones recientes han demostrado que las inestabilidades de este tipo desaparecen cuando una restricción regularizing o término de la pena está incorporado en el procedimiento de optimización.[12]
Supuestos
El marco de la MPT hace muchas suposiciones acerca de los inversores y los mercados. Algunos son explícitos en las ecuaciones, como el uso de Distribuciones normales a las declaraciones de la modelo. Otros están implícitos, tales como la negligencia de los impuestos y tasas de transacción. Ninguno de estos supuestos es totalmente cierto, y cada uno de ellos compromete MPT hasta cierto grado.
- Los inversionistas están interesados en el problema de optimización descrito anteriormente (maximizando la media para una determinada variación). En realidad, los inversores tienen funciones de utilidad que pueden ser sensibles a los momentos más altos de la distribución de los rendimientos. Para que los inversores utilizar la optimización de media-varianza, se debe suponer que la combinación de utilidad y rendimientos hacen la optimización del problema de utilidad relacionados con el problema de la optimización de media-varianza. Una utilidad cuadrática sin ninguna suposición acerca de devoluciones es suficiente. Otra hipótesis es utilizar la utilidad exponencial y distribución normal, como se explica más abajo.
- Retornos de activos son)conjuntamente) distribuye normalmente al azar variables. De hecho, con frecuencia se observa que devuelve en equidad y otros mercados no se distribuye normalmente. Grandes oscilaciones (3 a 6 las desviaciones estándar de la media) se producen en el mercado mucho más frecuentemente de lo que podría predecir la asunción de distribución normal.[13] Mientras que el modelo también puede justificarse asumiendo que cualquier retorno distribución conjuntamente elíptica,[14][15] todas las distribuciones elípticas conjuntas son simétricas mientras que devuelve activos empíricamente no es. Bouchaud y Chicheportiche (2012) [16] rechazan empíricamente la hipótesis elíptica, escribiendo "intuitivamente, el fracaso de los modelos elípticos puede rastrearse a la insuficiencia de la asunción de un modo único volatilidad de todas las poblaciones."
- Las correlaciones entre los activos son fijos y constantes para siempre. Correlaciones dependen de las relaciones sistémicas entre los activos subyacentes y cambian cuando cambian estas relaciones. Los ejemplos incluyen un país declarando la guerra a otro, o un desplome del mercado general. En tiempos de crisis financiera todos los activos tienden a convertirse en una correlación positiva, porque todos ellos se mueven juntos (abajo). En otras palabras, MPT rompe precisamente cuando los inversionistas están más necesitados de protección de riesgo.
- Todos los inversores tienen como objetivo maximizar la utilidad económica (en otras palabras, para hacer tanto dinero como sea posible, independientemente de cualquier otra consideración). Esta es una suposición fundamental de la hipótesis del mercado eficiente, sobre la cual se basa la MPT.
- Todos los inversionistas son racionales y los riesgos. Esta es otra hipótesis de la hipótesis del mercado eficiente. En realidad, como lo demuestra economía conductista, los participantes del mercado no siempre son racional o constantemente racional. La Asunción no tiene en cuenta para las decisiones emocionales, información sobre el mercado viejo, "el comportamiento de rebaño" o los inversionistas que pueden solicitar el riesgo por riesgo. Jugadores de Casino claramente pagar por riesgo, y es posible que algunos comerciantes stock pagará por riesgo.
- Todos los inversores tienen acceso a la misma información al mismo tiempo. De hecho, los mercados reales contienen asimetría en la información, privilegiada, y quienes son simplemente mejor informaron que los demás. Por otra parte, estimar la media (por ejemplo, no es ningún estimador consistente de la deriva de un browniano cuando submuestreo entre 0 y T) y la matriz de covarianza de los rendimientos (cuando el número de activos es del mismo orden del número de periodos) son tareas difíciles de estadísticas.
- Los inversores tienen una concepción exacta de los posibles retornos, es decir, las creencias de probabilidad de inversores coinciden con la verdadera distribución de los retornos. Otra posibilidad es que las expectativas de los inversores están prejuiciadas, causando que los precios de mercado que seamos ineficientes. Esta posibilidad se estudia en el campo de la Finanzas del comportamiento, que utiliza supuestos psicológicos para ofrecer alternativas a la CAPM como el activo basado en exceso de confianza precios modelo de Kent Daniel, David Hirshleifery Avanidhar Subrahmanyam (2001).[17]
- No existen impuestos o costos de transacción. Productos financieros reales están sujetos a impuestos y los costos de transacción (tales como los honorarios del agente), y tomando en cuenta esto alterará la composición de la cartera óptima. Estos supuestos pueden estar relajados con versiones más complicadas del modelo.[citación necesitada]
- Todos los inversionistas son tomadores de precios, es decir, sus acciones no influyen en los precios. En realidad, lo suficientemente grandes ventas o compras de activos individuales pueden cambiar los precios de mercado para ese activo y otros (a través de elasticidad cruzada de la demanda.) Un inversionista no puede incluso ser capaz de montar la cartera teóricamente óptima si el mercado mueve demasiado tiempo que están comprando los valores requeridos.
- Cualquier inversionista puede prestar y pedir prestado una cantidad ilimitada de la tasa libre de riesgo de interés. En realidad, cada inversionista tiene un límite de crédito.
- Todos los valores pueden dividirse en parcelas de cualquier tamaño. En realidad, acciones fraccionarias generalmente no pueden ser compradas o vendidas, y algunos activos tienen tamaños pedidos mínimos.
- Riesgo/volatilidad de un activo se conoce de antemano/es constante. De hecho, los mercados a menudo misprice de riesgo (por ejemplo Estados Unidos hipotecar la burbuja o la crisis de deuda europea) y volatilidad cambia rápidamente.
Versiones más complejas de MPT pueden tomar en cuenta un modelo más sofisticado del mundo (por ejemplo, uno con las distribuciones normales e impuestos), pero todos los modelos matemáticos de finanzas todavía dependen de muchos locales poco realistas.
MPT no modelo realmente el mercado
Las medidas de riesgo, retorno y correlación utilizadas por MPT se basan en valores esperados, lo que significa que son declaraciones matemáticas sobre el futuro (el valor esperado de los retornos es explícito en las ecuaciones anteriores e implícitos en las definiciones de varianza y covarianza). En la práctica, los inversores deben sustituir predicciones basadas en mediciones históricas de retorno activo y volatilidad para estos valores en las ecuaciones. Muy a menudo tales valores esperados no tener en cuenta nuevas circunstancias que no existían cuando se generaron los datos históricos.
Más fundamentalmente, los inversionistas se quedan con estimación de los parámetros clave de los últimos datos del mercado porque MPT intenta modelo riesgo en términos de la probabilidad de pérdidas, pero no dice nada acerca de por qué pueden ocurrir esas pérdidas. Las medidas de riesgo utilizadas son probabilística en la naturaleza, no estructural. Esta es una gran diferencia en comparación con muchos enfoques de ingeniería para gestión del riesgo.
Opciones teoría y MPT tienen al menos una diferencia conceptual importante de la evaluación probabilística del riesgo hecho por energía nuclear [plantas]. Un ERP es lo que los economistas llamaría un modelo estructural. Los componentes de un sistema y sus relaciones están modelados en Simulaciones Monte Carlo. Si falla la válvula X, causa una pérdida de presión en la bomba Y, causando una caída en el flujo al buque Z y así sucesivamente.
Pero en el Black-Scholes ecuación y MPT, no hay ningún intento de explicar una estructura subyacente a los cambios de precios. Varios resultados simplemente se dan las probabilidades. Y, a diferencia del PRA, si no hay ninguna historia de un evento particular de nivel del sistema como un crisis de liquidez, no hay ninguna manera de calcular las probabilidades de. Si ingenieros nucleares funcionaron la gestión de riesgos de esta manera, ellos nunca sería capaces de calcular las probabilidades de una crisis en una planta en particular hasta varios eventos similares ocurrieron en el mismo diseño del reactor.
— Douglas W. Hubbard, 'El fracaso de la gestión de riesgos', p. 67, John Wiley & Sons, 2009. ISBN 978-0-470-38795-5
Esencialmente, las matemáticas de la MPT ve los mercados como una colección de dados. Examinando más allá de los datos de mercado podemos desarrollar hipótesis sobre cómo se ponderan los dados, pero esto no es útil si los mercados dependen en realidad mucho más grande y más complicado caótico sistema — el mundo. Por esta razón, precisos modelos estructurales de los mercados financieros realmente están poco probable que darían porque esencialmente serían modelos estructurales de todo el mundo. Sin embargo existe una creciente conciencia del concepto de riesgo sistémico en los mercados financieros, que deben conducir a modelos más sofisticados del mercado.
Las mediciones de riesgo matemática también son útiles sólo en la medida en que reflejan verdaderas preocupaciones de los inversores — minimizando una variable que nadie le importa en la práctica no tiene sentido. MPT utiliza el concepto matemático de varianza para cuantificar el riesgo y esto podría justificarse bajo el supuesto de elíptico distribuidos devuelve como distribuye normalmente devoluciones, pero para el general volver distribuciones otras medidas de riesgo (como medidas de riesgo coherentes) podría reflejar mejor verdaderas preferencias de los inversionistas.
En particular, varianza es una medida simétrica que cuenta anormalmente alta tan sólo devuelve tan arriesgada como anormalmente bajos rendimientos. Algunos podrían argumentar que, en realidad, los inversionistas sólo están preocupados por las pérdidas y no se preocupan por la dispersión o devuelve tirantez de por encima del promedio. Según esta visión, nuestro concepto intuitivo de riesgo es fundamentalmente asimétrica en la naturaleza.
MPT no tiene en cuenta para el personal, ambiental, estratégico, o dimensiones sociales de las decisiones de inversión. Sólo intenta maximizar los retornos ajustados por riesgo, independientemente de otras consecuencias. En un sentido estricto, su dependencia completa de activos precios hace vulnerable a todos los estándar fallas del mercado como las derivadas de asimetría en la información, externalidades, y bienes públicos. También premia fraudes corporativos y contabilidad deshonesta. En términos más generales, una empresa puede tener objetivos estratégicos o sociales que dan forma a sus decisiones de inversión, y un inversor individual podría tener metas personales. En cualquier caso, es relevante información aparte de rentabilidades históricas.
Economista financiero Nassim Nicholas Taleb también ha criticado la teoría moderna de portafolio porque asume un Distribución Gausiana:
- Después de la caída del mercado de valores (en 1987), ellos recompensados a dos teóricos, Harry Markowitz y William Sharpe, quien construyó modelos bellamente platónicos sobre una base gaussiana, contribuyendo a lo que se denomina la teoría moderna de portafolio. Simplemente, si quita sus supuestos gaussianos y tratar precios como escalable, se queda uno con aire caliente. El Comité Nobel podría han probado el Sharpe y Markowitz modelos — trabajan como curandero remedios vendieron en Internet, pero parece que han pensado nadie en Estocolmo. [18] :: p.279
El MPT no tener en cuenta su propio efecto sobre los precios de los activos
Diversificación elimina el riesgo no sistemático. Como riesgo asistemático no está asociada con mayor rentabilidad esperada, esto es considerado uno de los pocos "almuerzos gratis" disponibles. Tras MPT significa gerentes de cartera pueden invertir en activos sin analizar sus fundamentos, especialmente ponderación cada activo por el peso de los mercados en el activo. Porque el inversionista compra activos en proporción a su peso de mercado, no hay ningún aumento relativo en la demanda de un activo versus otro, y así no devuelve ningún impacto en la esperada de la cartera.
Extensiones
Desde la introducción del MPT en 1952, se han hecho muchos intentos para mejorar el modelo, especialmente mediante el uso de supuestos más realistas.
Teoría posmoderna cartera se extiende el MPT mediante la adopción de medidas no-normalmente distribuidas, asimétricas de riesgo. Esto ayuda a algunos de estos problemas, pero otros no.
Modelo de Black-Litterman la optimización es una extensión de optimización sin restricciones de Markowitz que incorpora relativos y absolutos 'vistas' sobre los insumos de riesgo y devuelve.
Otras aplicaciones
Aplicaciones en carpetas de proyecto y otros activos "no financieros"
Algunos expertos aplican MPT a las carteras de proyectos y otros bienes además de los instrumentos financieros.[19][20] Cuando MPT se aplica fuera de carteras financieras tradicionales, se deben considerar algunas diferencias entre los distintos tipos de carpetas.
- Los activos en carteras financieras son, para propósitos prácticos, continuamente divisibles mientras carteras de proyectos son "bultos". Por ejemplo, mientras que nosotros podemos calcular que la cartera óptima posición para 3 poblaciones es, decir, 44%, 35%, 21%, la posición óptima para una cartera de proyectos que no nos permiten simplemente cambiar el monto gastado en un proyecto. Proyectos podrían ser todo o nada o, al menos, tener las unidades lógicas que no pueden ser separadas. Un método de optimización de cartera tendría que considerar la naturaleza discreta de proyectos.
- Los activos de las carteras financieras son líquidos; pueden ser evaluados o reevaluarse en cualquier punto en el tiempo. Pero las oportunidades para el lanzamiento de nuevos proyectos pueden ser limitadas y pueden ocurrir en windows limitados de tiempo. Proyectos que ya han sido iniciados no pueden ser abandonados sin la pérdida de la costos hundidos (es decir, hay poco o ningún valor de recuperación/recuperación de un proyecto de medias).
Ninguno de estos necesariamente eliminar la posibilidad de utilizar esas carteras y MPT. Simplemente indican la necesidad de ejecutar la optimización con un conjunto de restricciones expresadas matemáticamente que normalmente no se aplicará a las carteras financieras.
Además, algunos de los elementos más simples de la moderna teoría de la cartera son aplicables a prácticamente cualquier tipo de cartera. El concepto de captura de la tolerancia al riesgo del inversionista por documentar cuánto riesgo es aceptable para un determinado retorno puede aplicarse a una variedad de problemas de análisis de decisión. MPT utiliza variación histórica como una medida de riesgo, pero carteras de activos como grandes proyectos no tienen una variación histórica de"bien definida". En este caso, el límite de inversión de MPT puede expresarse en términos más generales como "la oportunidad de un ROI menos costo de capital" o "la oportunidad de perder más de la mitad de la inversión". Cuando se pone riesgo en términos de incertidumbre acerca de las previsiones y posibles pérdidas y el concepto es transferible a varios tipos de inversión.[19]
Aplicación a otras disciplinas
En la década de 1970, conceptos de la teoría moderna de portafolio encontraron su camino en el campo de la ciencia regional. En una serie de obras seminales, Michael Conroy[citación necesitada] modelo de la fuerza laboral en la economía mediante métodos cartera teórica para examinar el crecimiento y la variabilidad en la fuerza laboral. Esto fue seguido por una larga literatura sobre la relación entre crecimiento económico y la volatilidad.[21]
Más recientemente, la teoría moderna de portafolio se ha utilizado para modelar el autoconcepto en la psicología social. Cuando los atributos del uno mismo que comprende el autoconcepto constituyen una cartera bien diversificada, entonces los resultados psicológicos a nivel del individuo como el estado de ánimo y la autoestima deben ser más estables que cuando el autoconcepto está diversificado. Esta predicción ha sido confirmada en estudios en seres humanos.[22]
Recientemente, se ha aplicado la teoría moderna de portafolio al modelado de la incertidumbre y la correlación entre documentos en la recuperación de información. Ante una consulta, el objetivo es maximizar la relevancia global de una lista ordenada de documentos y al mismo tiempo minimizar la incertidumbre global de la lista ordenada.[23]
Comparación con arbitraje de precios teoría
La línea del mercado de seguridad y modelo de precios de activos de capital a menudo son contrastadas con el arbitraje teoría de precios (APT), que sostiene que el retorno esperado de un activo financiero puede ser modelada como una función lineal de varios macroeconómicas factores, donde la sensibilidad a los cambios en cada factor está representada por un factor específico coeficiente beta.
La APT es menos restrictiva en sus hipótesis: permite un modelo estadístico de los retornos de activos y asume que cada inversionista tendrá una cartera única con su propio conjunto particular de betas, en comparación con el idéntico "cartera de mercado". A diferencia del CAPM, la APT, sin embargo, no se revela la identidad de sus factores de precio, el número y la naturaleza de estos factores es probable que cambie con el tiempo y entre las economías.
Véase también
- Polarización ratio (finanzas)
- Modelo de Black-Litterman
- Análisis fundamental
- Elección intertemporal cartera
- Teoría de la inversión
- Alfa de Jensen
- Marginal condicional dominancia estocástica
- Teorema de separación de fondos mutuos
- Teoría posmoderna cartera
- Crítica del rodillo
- Sortino ratio
- Relación Treynor
- Modelos de decisión de momento dos
- Valor inversión
- Anomalía de baja volatilidad
Referencias
- ^ Harry M. Markowitz - autobiografía, los premios Nobel 1990, Editor Tore Frängsmyr, [Nobel Foundation], Stockholm, 1991
- ^ "Managed Futures - reducir la volatilidad de la cartera | Un vistazo a los mejores futuros gestionados 3 cuentas en todo el mundo". 19 / 03 / 2011 Emanagedfutures.com.. 2012-09-05.
- ^ Bhalla, K. V. (2010). Gestión de inversiones. Nueva Delhi: S. Chand y Co. págs. 587 – 93. ISBN81-219-1248-2.
- ^ Andrei Shleifer: Mercados ineficientes: una introducción a las finanzas del comportamiento. Clarendon conferencias en economía (2000)
- ^ Koponen, Timothy M. 2003. Materias primas en acción: medición de arraigo y la imposición de valores. La revisión sociológica. Volumen 50 número 4, páginas 543-569
- ^ Jenson, Michael; Scholes, Myron; Negro, Fischer (1972). "El Capital Asset Pricing modelo: algunas pruebas empíricas". En Jensen, Michael. Estudios en la teoría de los mercados de capitales. Praeger Publishers. 24 / 03 / 2014 obtenido.
- ^ a b c Edwin J. Elton y Martin J. Gruber, "teoría de cartera moderna, 1950 hasta la fecha", Journal of Banking & Finance 21 (1997) 1743-1759
- ^ Markowitz, H.M. (marzo de 1952). "Selección de cartera". El diario de finanzas 7 (1): 77-91. Doi:10.2307/2975974. JSTOR2975974.
- ^ Markowitz, H.M. (1959). Selección de cartera: Eficiente diversificación de inversiones. Nueva York: John Wiley & Sons. (Reimpreso por Yale University Press, 1970, ISBN 978-0-300-01372-6; 2ª ed. Basil Blackwell, 1991, ISBN 978-1-55786-108-5)
- ^ a b c Merton, Robert. "Una derivación analítica de la frontera eficiente de cartera" Diario financiero y análisis cuantitativo 7 de septiembre de 1972, 1851-1872.
- ^ Mahdavi Damghani B. (2013). "El valor de correlación inferido no induzcan a error: una introducción al modelo de Cointelation". Wilmott Magazine. Doi:10.1002/Wilm.10252.
- ^ Brodie, De Mol, Daubechies, Giannone y Loris (2009). "Carteras de Markowitz escasos y estables". Actas de la Academia Nacional de Ciencias 106 (30). Doi:10.1073/pnas.0904287106.
- ^ Mandelbrot, B. y Hudson, R. L. (2004). Comportamiento de los mercados (Mis): una vista Fractal del riesgo, ruina y la recompensa. Londres: Perfil libros.
- ^ Chamberlain, g. 1983."Una caracterización de las distribuciones que implican funciones de utilidad media varianza", Journal of Economic Theory 29, 185-201.
- ^ Owen, J.; Rabinovitch, R. (1983). "En la clase de distribuciones elípticas y sus aplicaciones a la teoría de la elección de cartera". Revista de finanzas 38:: 745-752. Doi:10.1111/j.1540-6261.1983.tb02499.x.
- ^ https://arxiv.org/pdf/1009.1100.pdf Chicheportiche, R. & Bouchaud, J. P. (2012). La distribución conjunta de los retornos de las acciones no es elíptica. International Journal of Finance teórica y aplicada, 15(03).
- ^ 'Exceso de confianza, arbitraje y equilibrio Asset Pricing,' Kent D. Daniel, David Hirshleifer y Avanidhar Subrahmanyam, Journal of Finance, 56(3) (junio de 2001), págs. 921-965
- ^ Taleb, Nassim Nicholas (2007), El cisne negro: El impacto de lo altamente ImprobableRandom House, ISBN 978-1-4000-6351-2.
- ^ a b Hubbard, Douglas (2007). ¿Cómo medir cualquier cosa: encontrar el valor de los Intangibles en los negocios. Hoboken, NJ: John Wiley & Sons. ISBN978-0-470-11012-6.
- ^ Sabbadini, Tony (2010). "Teoría de la cartera de fabricación". Instituto Internacional de estudios avanzados en sistemas de investigación y cibernética.
- ^ Chandra, Siddharth (2003). "Tamaño de la economía regional y la frontera de crecimiento-inestabilidad: evidencia de Europa". Journal of Regional Science 43 (1): 95-122. Doi:10.1111/1467-9787.00291.
- ^ Chandra, Siddharth; Shadel, William G. (2007). "Cruzar los límites disciplinarios: aplicando teoría de cartera financiera para la organización del autoconcepto del modelo". Revista de investigación en personalidad 41 (2): 346 – 373. Doi:10.1016/j.JRP.2006.04.007.
- ^ Teoría de la cartera de recuperación de información 11 de julio de 2009 (2009-07-11). "Teoría de la cartera de recuperación de información | Página de inicio de Dr. Jun Wang". Web4.cs.UCL.AC.uk. 2012-09-05.
Lectura adicional
- Lintner, John (1965). "La valoración de activos de riesgo y la selección de las inversiones riesgosas en carteras de acciones y presupuestos de Capital". La revisión de la economía y estadística (El MIT Press) 47 (1): 13-39. Doi:10.2307/1924119. JSTOR1924119.
- Sharpe, William F. (1964). "Precios de los activos de Capital: una teoría de equilibrio de mercado bajo condiciones de riesgo". Revista de finanzas 19 (3): 425-442. Doi:10.2307/2977928. JSTOR2977928.
- Tobin, James (1958). "Preferencia de liquidez como el comportamiento hacia el riesgo". La revisión de estudios económicos 25 (2): 65-86. Doi:10.2307/2296205. JSTOR2296205.
Enlaces externos
- Análisis de macro-inversiones, Prof. William Sharpe F., Stanford
- Una introducción a la teoría de inversiónProf. William N. Goetzmann, Yale School of Management
- Markowitz Portfolio selección en Excel
- Markowitz Portfolio optimización en línea
- Teoría moderna de portafolio
- Utilizar el simuaton Monte Carlo para enseñar MPT
|
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||

 es el retorno de la cartera,
es el retorno de la cartera,
 es el retorno sobre activos
i y
es el retorno sobre activos
i y
 es la ponderación del componente activo
es la ponderación del componente activo
 (es decir, la proporción del activo "i" de la cartera).
(es decir, la proporción del activo "i" de la cartera).
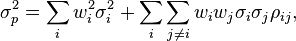
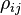 es el coeficiente de correlación entre los rendimientos de los activos
i y
j. Alternativamente la expresión puede ser escrita como:
es el coeficiente de correlación entre los rendimientos de los activos
i y
j. Alternativamente la expresión puede ser escrita como:
 ,
,
 para
i=
j.
para
i=
j.





 , se encuentra la frontera eficiente reduciendo al mínimo la siguiente expresión:
, se encuentra la frontera eficiente reduciendo al mínimo la siguiente expresión:
 es un vector de pesos de cartera y
es un vector de pesos de cartera y  (Los pesos pueden ser negativos, lo que significa que los inversores pueden corto seguridad.);
(Los pesos pueden ser negativos, lo que significa que los inversores pueden corto seguridad.); es el matriz de covarianza para los rendimientos de los activos de la cartera;
es el matriz de covarianza para los rendimientos de los activos de la cartera; es un factor "riesgo de tolerancia", donde 0 resultados en la cartera con riesgo mínimo y
es un factor "riesgo de tolerancia", donde 0 resultados en la cartera con riesgo mínimo y  resultados de la cartera infinitamente lejos de la frontera con rentabilidad esperada y riesgo sin límites; y
resultados de la cartera infinitamente lejos de la frontera con rentabilidad esperada y riesgo sin límites; y es un vector de retornos esperados.
es un vector de retornos esperados.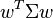 es la varianza de la cartera de retorno.
es la varianza de la cartera de retorno. es el retorno esperado de la cartera.
es el retorno esperado de la cartera. Esta versión del problema requiere que minimizamos
Esta versión del problema requiere que minimizamos
 . Este problema se soluciona fácilmente usando un Multiplicadores de Lagrange.
. Este problema se soluciona fácilmente usando un Multiplicadores de Lagrange.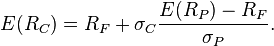

 Beta, es la medida de la sensibilidad de activos a un movimiento en el mercado en general; Beta se encuentra generalmente vía regresión en los datos históricos. Betas superior a uno significan contribución promedio más de "riesgo" en el sentido de los activos riesgo de la cartera total; betas debajo de uno indican un más bajo que la contribución de riesgo medio.
Beta, es la medida de la sensibilidad de activos a un movimiento en el mercado en general; Beta se encuentra generalmente vía regresión en los datos históricos. Betas superior a uno significan contribución promedio más de "riesgo" en el sentido de los activos riesgo de la cartera total; betas debajo de uno indican un más bajo que la contribución de riesgo medio. es la prima de mercado, la rentabilidad esperada de excesiva de la cartera mercado espera regresar sobre la tasa libre de riesgo.
es la prima de mercado, la rentabilidad esperada de excesiva de la cartera mercado espera regresar sobre la tasa libre de riesgo.![(w_m^2 \sigma_m ^2 + [ w_a^2 \sigma_a^2 + 2 w_m w_a \rho_{am} \sigma_a \sigma_m] )](http://upload.wikimedia.org/math/8/a/6/8a6c334e7488d54d5e86b762664ac768.png)
![[ w_a^2 \sigma_a^2 + 2 w_m w_a \rho_{am} \sigma_a \sigma_m]](http://upload.wikimedia.org/math/0/6/5/065759bd620995bdd1a7653abf3f9047.png)
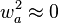
![[ 2 w_m w_a \rho_{am} \sigma_a \sigma_m] \quad](http://upload.wikimedia.org/math/5/b/1/5b146f9f3dfe9825bef30e7fbb900c64.png)
![( w_m \operatorname{E}(R_m) + [ w_a \operatorname{E}(R_a) ] )](http://upload.wikimedia.org/math/c/4/2/c420bcc15433abfb8180d580508e3995.png)
![[ w_a \operatorname{E}(R_a) ]](http://upload.wikimedia.org/math/2/9/2/292f0f3fd92a3bdf1fa91cc492cecda0.png)
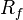 ; Esto es racional si
; Esto es racional si  .
.![[ w_a ( \operatorname{E}(R_a) - R_f ) ] / [2 w_m w_a \rho_{am} \sigma_a \sigma_m] = [ w_a ( \operatorname{E}(R_m) - R_f ) ] / [2 w_m w_a \sigma_m \sigma_m ]](http://upload.wikimedia.org/math/e/8/d/e8db53a1d6ccf7f92d3172ca2d6513c9.png)
![[\operatorname{E}(R_a) ] = R_f + [\operatorname{E}(R_m) - R_f] * [ \rho_{am} \sigma_a \sigma_m] / [ \sigma_m \sigma_m ]](http://upload.wikimedia.org/math/c/f/d/cfdeeddd7d3731cb61a106fbe18a9766.png)
![[\operatorname{E}(R_a) ] = R_f + [\operatorname{E}(R_m) - R_f] * [\sigma_{am}] / [ \sigma_{mm}]](http://upload.wikimedia.org/math/b/3/b/b3b928bc81cc747286a4008802276277.png)
![[\sigma_{am}] / [ \sigma_{mm}] \quad](http://upload.wikimedia.org/math/1/0/6/1067daf771684197f14d2f245550c2dc.png) es la "beta",
es la "beta",