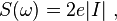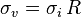Ruido de disparo

Simulación de ruido del fotón.

Ruido de disparo es un tipo de ruido electrónico que origina de la naturaleza discreta de carga eléctrica. El término también se aplica al fotón contando en dispositivos ópticos, donde tiro ruido está asociada con la naturaleza de la partícula de la luz.

Origen

Es sabido que en un experimento estadístico como lanzar una moneda justa y contando las ocurrencias de cabezas y colas, el número de cabezas y colas después de un gran muchos tiros diferirá por sólo un pequeño porcentaje, mientras que después de sólo unos pocos tiros los resultados con un exceso significativo de cabezas sobre colas o viceversa es comunes; Si un experimento con unos tiros se repite una y otra vez, los resultados a fluctuar mucho. (Puede ser probado que reducen las fluctuaciones relativas como la raíz cuadrada del número de tiros, un resultado válido para fluctuaciones todos estadísticas, incluyendo tiro ruido).

Ruido de disparo existe porque fenómenos como la corriente eléctrica y luz consisten en el movimiento de discretos (también llamado "quantized") 'paquetes'. Considerar la luz — una corriente de fotones discretos — saliendo de un puntero láser y chocar contra un muro para crear un lugar visible. Los procesos físicos fundamentales que rigen la emisión de luz son tales que estos fotones se emiten desde el láser a veces al azar; Pero los muchos miles de millones de fotones necesitados para crear un lugar son tantos que el brillo, el número de fotones por unidad de tiempo, sólo infinitesimalmente varía con el tiempo. Sin embargo, si el brillo del laser es reducido hasta sólo un puñado de fotones golpeó la pared cada segundo, las fluctuaciones relativas en número de fotones, es decir, brillo, será significativo, al igual que al lanzar una moneda de un par de veces. Estas fluctuaciones son rodadas ruido.

El concepto de ruido tiro introdujo por primera vez en 1918 por Walter Schottky que estudió las fluctuaciones de la corriente en tubos de vacío.

Tiro el ruido puede ser dominante cuando el número finito de partículas que transportan la energía (tales como electrones en un circuito electrónico o fotones en un dispositivo óptico) es lo suficientemente pequeño para que las incertidumbres debido a la Distribución de Poisson, que describe la ocurrencia de eventos aleatorios independientes, son de importancia. Es importante en electrónica, telecomunicaciones, detección ópticay fundamental física.

El término también puede usarse para describir a cualquier fuente de ruido, aunque únicamente matemática, de origen similar. Por ejemplo, simulaciones de partículas pueden producir una cierta cantidad de "ruido", donde debido al escaso número de partículas simulado, la simulación exhibe excesivas fluctuaciones estadísticas que no reflejan el sistema del mundo real. La magnitud del ruido tiro aumenta según la raíz cuadrada del número esperado de eventos, como la corriente eléctrica o intensidad de la luz. Pero puesto que la intensidad de la señal se aumenta más rápidamente, el relativa proporción de ruido de disparo disminuye y la señal / ruido de todos modos aumenta (considerando solo tiro ruido). Así ruido de disparo se observó con mayor frecuencia con pequeñas corrientes o intensidades de luz tras amplificación suficiente.

El número de fotones que son recogidos por un detector de determinado varía y sigue un Distribución de Poisson, representada aquí por los promedios de 1, 4 y 10.

Para un gran número se acerca a la distribución de Poisson a distribución normal, normalmente haciendo ruido tiro en observaciones reales indistinguible de la verdad Ruido gaussiano salvo cuando son tan pocos que individualmente se observan los eventos elementales (fotones, electrones, etc.). Puesto que el desviación estándar ruido de disparo es igual a la raíz cuadrada del número promedio de eventos N, la relación señal / ruído (SNR) viene dada por:

$\mathrm{SNR} = \frac{N}{\sqrt{N}} = \sqrt{N}. \,$

Por lo tanto cuando N es muy grande, que la relación señal a ruido es muy grande, y cualquier relativa fluctuaciones en N debido a otras fuentes son más propensos a dominar sobre ruido de disparo. Sin embargo cuando la otra fuente de ruido está en un nivel fijo, tales como ruido térmico, aumentando N (el nivel actual o Luz DC, etc). a veces puede conducir a la dominación de tiro ruido sin embargo.

Propiedades

Dispositivos electrónicos

Ruido de disparo en los circuitos electrónicos se compone de las fluctuaciones aleatorias de la corriente eléctrica en un DC corriente que se originan debido al hecho de que corriente en realidad consiste en un flujo de discreta cobra)electrones). Debido a que el electrón tiene una carga tan pequeña, sin embargo, ruido de disparo es de relativa insignificancia en muchas (pero no todos) los casos de conducción eléctrica. Por ejemplo 1 Ampere de corriente consiste en sobre 6.24×10¹⁸ electrones por segundo; Aunque este número al azar variará según varios millones en cualquier momento dado, tal una fluctuación es minúscula en comparación con la corriente de sí mismo. Además, ruido de disparo es a menudo menos significativo en comparación con otras dos fuentes de ruido en circuitos electrónicos, ruido de parpadeo y Ruido de Johnson-Nyquist. Sin embargo, tiro el ruido es temperatura y frecuencia independiente, en contraste con el ruido de Johnson-Nyquist, que es proporcional a la temperatura y ruido de parpadeo, con la densidad espectral disminuye con la frecuencia. Por lo tanto en las frecuencias altas y bajas temperaturas, ruido de disparo puede convertirse en la fuente dominante de ruido.

Considerando un tiempo más corto y con corrientes muy pequeñas escalas (por lo tanto más amplio ancho de banda) ruido de disparo pueden ser significativas. Por ejemplo, un circuito de microondas opera en escalas de tiempo de menos de un nanosegundo y si fuéramos a tener una corriente de 16 nanoamperes Eso equivaldría a sólo 100 electrones pasando cada nanosegundo. Según Estadísticas de Poisson el real número de electrones en cualquier nanosegundo variaría por 10 electrones RMS, así que un sexto del tiempo menos de 90 electrones pasaría un punto y una sexta parte del tiempo más de 110 electrones contados en un nanosegundo. Ahora con esta pequeña corriente vistos en esta escala de tiempo, las cantidades de ruido de disparo a 1/10 de la DC actual sí mismo.

El resultado de Schottky, basado en la suposición de que las estadísticas de paso de los electrones es Poissonian, Lee para la densidad espectral del ruido en la frecuencia $\omega$,

$S (\omega) = 2e\vert I \vert \ ,$

donde $e$ es la carga del electrón, y $I$ el promedio actual es creado por la corriente de electrones. La potencia espectral de ruido es frecuencia independiente, lo cual significa que el ruido es Blanco. Este es el clásico resultado en el sentido de que no toma en cuenta que los electrones obedecen Estadística de Fermi-Dirac. 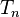Esto puede combinarse con la Fórmula de Landauer, que refiere la media actual con el valores propios de la transmisión $T_n$ del contacto a través del cual la corriente es medido ($n$ Etiquetas canales de transporte). En el caso más simple estos valores propios de la transmisión se pueden tomar energía independiente, es la fórmula de Landauer

$I = \frac{e^2}{\pi\hbar} V \sum_n T_n \ ,$

donde $V$ es la tensión aplicada. Esto proporciona para

$S = \frac{2e^3}{\pi\hbar} \vert V \vert \sum_n T_n \ ,$

comúnmente conocido como el valor de Poisson de ruido de disparo, $S_P$. El resultado correcto toma en cuenta la estadística cuántica de electrones y Lee (a temperatura cero)

$S = \frac{2e^3}{\pi\hbar} \vert V \vert \sum_n T_n (1 - T_n)\ .$

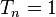Se obtuvo en la década de 1990 por Khlus, Lesovik (independientemente del caso solo canal), y Büttiker (caso de multicanal). Este ruido es blanco y siempre se suprime con respecto al valor de Poisson. El grado de represión, $F = S/S_P$, es conocido como el Factor de Fano. Sonidos producidos por los canales de transporte son independientes. Completamente abierta)$T_n=1$) y totalmente cerrado ()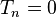$T_n=0$) canales de producen ningún ruido, puesto que no hay ninguna irregularidad en el flujo de electrones.

A temperatura finita, se puede escribir una expresión cerrada para el ruido. Interpola entre ruido (cero temperatura) y ruido de Johnson-Nyquist (alta temperatura).

Ejemplos

• Cruce de túnel se caracteriza por la baja transmisión en todos los canales de transporte, por lo tanto el flujo del electrón es Poissonian, y el factor de Fano es igual a uno.
• Contacto de punto cuántico se caracteriza por una transmisión ideal en canales abiertos, por lo tanto no produce ningún ruido, y el factor de Fano es igual a cero. La excepción es el paso entre mesetas, cuando uno de los canales está parcialmente abierto y produce un ruido.
• Un alambre metálico difusivo tiene un factor de Fano de 1/3 independientemente de la geometría y los detalles del material.
• En 2DEG exhibiendo efecto Hall cuántico fraccionario corriente eléctrica es llevada por quasiparticles moviéndose en el borde de la muestra, cuyo cargo es una fracción racional de la carga del electrón. La primera medición directa de su carga fue por el ruido de disparos en la corriente.

Efectos de las interacciones

Mientras que esto es el resultado cuando los electrones que contribuyen a la corriente se producen completamente al azar, inafectado por los demás, hay importantes casos en los que estas fluctuaciones naturales se suprimen en gran parte debido a una acusación de construcción. Tomemos el ejemplo anterior en el que un promedio de 100 electrones ir del punto al punto B cada nanosegundo. Durante la primera mitad de un nanosegundo esperaríamos 50 electrones para llegar al punto B en el promedio, pero en un determinado medio nanosegundo bien podría haber 60 electrones que llegan allí. Esto creará una carga eléctrica negativa más en el punto B que el promedio, y ese recargo tenderán a repeler el mayor flujo de electrones abandone punto A durante la restante mitad nanosegundo. Así la corriente neta integrada sobre un nanosegundo tenderán más a permanecer cerca de su valor promedio de 100 electrones en lugar de exhibir las fluctuaciones esperadas (10 electrones rms) se calculó. Este es el caso en los alambres metálicos ordinarios y de película metálica resistencias, donde el ruido de disparo es casi totalmente cancelado debido a este anti-correlación entre el movimiento de electrones individuales, actuando el uno al otro a través de la fuerza del culombio.

Sin embargo esta reducción de ruido de disparo no se aplica cuando el actual resultado de eventos aleatorios en una barrera de potencial que deben superar todos los electrones debido a una excitación al azar, como por la activación térmica. Esta es la situación en uniones p-n, por ejemplo. Un semiconductor diodo por lo tanto utiliza comúnmente como una fuente de ruido aprobando un particular DC actual a través de él.

Ruido de disparo es distinta de voltaje y corriente fluctuaciones esperadas en equilibrio térmico; Esto ocurre sin ninguna tensión DC o corriente que fluye. Estas fluctuaciones son conocidas como Ruido de Johnson-Nyquist o ruido termal y aumentar proporcionalmente a la Kelvin temperatura de cualquier componente resistiva. Sin embargo ambos son instancias de ruido blanco y por lo tanto no se pueden distinguir simplemente observando los aunque sus orígenes son muy diferentes.

Puesto que el ruido shot es un Proceso de Poisson debido a la carga finita de un electrón, uno puede computar la media cuadrática fluctuaciones de corriente por ser de una magnitud

$\sigma_i=\sqrt{2\,q\,I\,\Delta f}$

donde q es el carga elemental de un electrón, Δf es el ancho de banda en Hertz sobre que el ruido es considerado, y I es la corriente que fluye.

Para una corriente de 100 mA, medir el ruido actual sobre un ancho de banda de 1 Hz, obtenemos

$\sigma_i = 0.18\,\mathrm{nA} \; .$

Si este ruido actual es alimentado a través de un resistor de una tensión de ruido de

$\sigma_v = \sigma_i \, R$

se generarían. Este ruido a través de un condensador de acoplamiento, uno podría suministrar una potencia de ruido de

$P = {\frac 1 2}\,q\,I\,\Delta f R.$

a una carga emparejada.

Óptica

En óptica, tiro ruido describe las fluctuaciones del número de fotones detectados (o simplemente contados en abstracto) debido a su ocurrencia independiente unos de otros. Por lo tanto es otra consecuencia de discretización, en este caso de la energía en el campo electromagnético en términos de fotones. En el caso del fotón detección, el proceso relevante es la conversión al azar de fotones en electrones-foto por ejemplo, lo que conduce a un mayor nivel de ruido tiro eficaz cuando se utiliza un detector con una eficiencia cuántica por debajo de la unidad. Sólo en un exótico estado coherente exprimido el número de fotones medidos por unidad de tiempo tengan fluctuaciones más pequeño que la raíz cuadrada del número esperado de fotones contados en ese período de tiempo. Por supuesto hay otros mecanismos de ruido en las señales ópticas que a menudo eclipsan la contribución del ruido de disparo. Cuando éstos están ausentes, sin embargo, detección óptica se dice que es ""fotón ruido limitado"que sólo los restos de ruido tiro (también conocido como"ruido cuántico"o"ruido de fotones"en este contexto).

Ruido de disparo es fácilmente observable en el caso de fotomultiplicadores y Fotodiodos de avalancha utilizado en el modo de Geiger, donde se observan las detecciones de fotones individuales. Sin embargo la misma fuente de ruido está presente con más altas intensidades de luz medidas por cualquiera detector de fotoy es directamente mensurable cuando domina el ruido del amplificador electrónico posterior. Igual que con otras formas de ruido de disparo, las fluctuaciones de una foto-actual debido al ruido de disparo de la escala como la raíz cuadrada de la intensidad media:

$\Delta I^2 \ \stackrel{\mathrm{def}}{=}\ \langle\left(I-\langle I\rangle \right)^2\rangle \propto I.$

El ruido de disparo de una viga óptica coherente (teniendo no otras fuentes de ruido) es un fenómeno físico fundamental, reflejando fluctuaciones cuánticas en el campo electromagnético (debido a la supuesta energía de punto cero). Esto establece un límite inferior sobre el ruido introducido por Amplificadores Quantum que preservar la fase de una señal óptica.

Véase también

• Ruido de Johnson-Nyquist o ruido termal
• ruido 1/f
• Ruido de explosión
• Ruido de imagen
• Eficiencia cuántica

Referencias

Este artículo incorporamaterial de dominio público desde el Administración de servicios generales documento "Federal estándar 1037C" (en apoyo de MIL-STD-188).

Enlaces externos

• Ruido de disparo en arxiv.org

Otras Páginas

• Domiciliacion bancaria
• RF64
• El desapalancamiento
• Alimentos para peces acuario
• Mogilyane
• Febrero de 2006 en la Union Europea
• J. Louis Watkins Jr.
• Cobitis bilseli
• Campimeter
• Guia de diez