Retorno esperado
|
|
Este artículo Necesita referencias adicionales para verificación. (Mayo de 2014) |
El retorno esperado (o ganancia esperada) se refiere al valor de una variable aleatoria uno podría esperar que si el proceso de encontrar la variable aleatoria podría ser repetido infinidad de veces. Formalmente, da la medida del centro de la distribución de la variable.[1]
Se calcula utilizando la siguiente fórmula:
![E[R]= \sum_{i=1}^{n}R_{i}P_{i}](http://upload.wikimedia.org/math/b/c/3/bc3a452977705030a6bd411b1b21f5ba.png) , donde:
, donde:
-
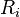 es el retorno en escenario
es el retorno en escenario
 ;
;
-
 es la probabilidad para el retorno
es la probabilidad para el retorno
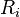 en escenario
en escenario
 ; y
; y
-
 cuenta el número de escenarios.
cuenta el número de escenarios.
Aunque esto es lo que uno espera el regreso a ser, esto sólo se refiere a la media a largo plazo. En el corto plazo, cada instancia del evento puede ser muy diferente. Como se indica por la fórmula anterior, simplemente tomar la probabilidad de cada resultado posible retorno y multiplíquelo por el resultado devuelto sí mismo. Por ejemplo, si uno sabía que una determinada inversión tenía un 50% de probabilidades de obtener un rendimiento de 10, un 25% de probabilidades de ganar 20 y un 25% de probabilidades de ganar – 10, la rentabilidad esperada sería igual a 7.5:
![E[R]=R_{1}P_{1} + R_{2}P_{2} + R_{3}P_{3} = 10*0.5 + 20*0.25 + (-10)*0.25 = 7.5.](http://upload.wikimedia.org/math/1/b/1/1b1b3d1b35df1e521d8056ba9683b1ff.png)
Aunque esto es lo que uno espera el regreso a ser, no hay ninguna garantía de que será el retorno real.
Contenido
- 1 Escenarios discretos
- 2 Escenarios continuas
- 3 Definición alternativa
- 4 Véase también
- 5 Notas
- 6 Enlaces externos
Escenarios discretos
En Juegos de azar y teoría de la probabilidad, suele haber un discreto conjunto de posibles resultados. En este caso, rentabilidad esperada es una medida del equilibrio relativo de ganar o pérdida ponderados por sus posibilidades de que ocurra.
Por ejemplo, si un muere justo se lanza y números 1 y 2 ganan $1, pero perder $0,5 a 3-6, entonces la ganancia esperada por tiro es ![E[R] = \frac{1}{3} \cdot 1 - \frac{2}{3} \cdot 0.5 = 0.](http://upload.wikimedia.org/math/7/1/0/710783897cde973ecff5ccb99da146f7.png)
Cuando calculamos la rentabilidad esperada de la inversión permite compararlo con otras oportunidades. Por ejemplo, teníamos la opción de elegir entre 3 inversiones; uno tiene un 60% de posibilidades de éxito y si consigue dará un 70% ROR. La segunda inversión tiene un 45% de posibilidades de éxito con un 20% ROR. La tercera oportunidad tiene un 80% de probabilidades de éxito con un 50% ROR. Para cada inversión, si no tiene éxito el inversor perderá su inversión inicial.
- La fórmula de la primera inversión es (.6 *.7) - (.4 * 1) =. 2% espera ROR
- La fórmula de la segunda inversión es (45 *.2) - (.55 * 1) = - 46% espera ROR
- La fórmula para la tercera inversión es (.8 *.5) - (2 * 1) = 20% espera ROR
Estos cálculos muestran que en nuestro escenario la tercera inversión es la más rentable de los tres. El segundo ni siquiera tiene un negativo ROR. Esto significa que si esa inversión se realizó una infinita cantidad de veces podría esperar a perder el 46% del dinero que invirtió. La fórmula del valor esperado es muy sencilla, pero su valor depende de las entradas. Los más factores que pueden influir en la inversión, las más variables en la ecuación. Como Ilmanen dijo,
"Es la necesidad más importante para el pensamiento multidimensional en las entradas. Cuando los inversionistas hacen juicios sobre los diferentes rendimientos de inversiones, que deben protegerse contra ceguera por rendimiento pasado y deben garantizar que se tomen todos o la mayoría de las siguientes consideraciones en cuenta".[2]
- Los rendimientos promedio históricos
- Teorías del comportamiento y financieras
- Adelante buscando indicadores del mercado tales como los bonos; y
- Discrecionales views
Escenarios continuas
En economía y Finanzas, es más probable que el conjunto de resultados posibles es continuo (un valor numérico o moneda entre 0 e infinito). En este caso, se hacen suposiciones simplificadoras sobre la distribución de los posibles resultados. Se construye una función de probabilidad continua, o se supone una distribución de probabilidad discreta
Definición alternativa
En finanzas, rentabilidad esperada también puede significar el retorno de un bono si paga la fianza. Es más el máximo retorno posible, aunque también puede ser la mediana o "esperaba más". Esto siempre será mayor que la rentabilidad esperada en el otro sentido presentado en este artículo porque el bono de pago es el mayor escenario de pago, y siempre es posible fracaso.
Véase también
- Retorno anormal
- Valor esperado
- Tasa de retorno
Notas
- ^ "Valor esperado como un aspecto Fundamental de la inversión".
- ^ Antti Ilmanen (2013). "Resumen, rentabilidades históricas y teorías académicas". Espera devuelve guía del inversionista al mercado recompensas. Wiley. p. 5. ISBN1119990726.
Enlaces externos
- Usando el retorno esperado para maximizar el crecimiento
- Calculadora de retorno esperado
Otras Páginas
- Jose Ruben
- Yaropolk Izyaslavich
- Alan Eagleson (abogados de categoria Disbarred)
- Nokia Lumia 625
- Seguridad publica respondiendo punto
- Banco comercial de Congo
- Cansema
- Real Compania de seguros de Malawi
- Motor Nissan Z
- Pedro Zamora (articulos de la categoria con hCards)
- Ambar gris
- Asociacion Nacional del Rifle
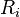 es el retorno en escenario
es el retorno en escenario
 ;
;
 es la probabilidad para el retorno
es la probabilidad para el retorno