Medida del riesgo entrópica
|
Este artículo proporciona contexto insuficiente para aquellos no familiarizados con el tema. (Julio de 2010) |
|
|
Este artículo también puede ser técnica para la mayoría de los lectores a entender. (Septiembre de 2010) |
Medida del riesgo entrópica es una posible medida del riesgo para usar en el contexto de la medición del riesgo como una alternativa a otras medidas de riesgo como Value-at-risk o déficit esperado. En matemáticas financieras, la medida del riesgo entrópica es un medida del riesgo que depende de la aversión al riesgo del usuario a través de la utilidad exponencial función. Esto representa una medida interesante teóricamente porque proporcionaría los valores de riesgo diferentes para diferentes personas. Sin embargo, en la práctica sería difícil de usar ya que la cuantificación de la aversión al riesgo de un individuo es difícil de hacer. La medida del riesgo entrópica es el mejor ejemplo de un medida del riesgo convexo que no es coherente.[1] Dada la conexión a funciones de utilidad Ya es una elección obvia para las limitaciones en problemas de maximización de utilidad.
Contenido
- 1 Definición matemática
- 2 Conjunto de aceptación
- 3 Medida del riesgo entrópico dinámico
- 4 Véase también
- 5 Referencias
Definición matemática
La medida del riesgo entrópica con el parámetro de aversión al riesgo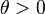 
se define como
-
![\rho^{\mathrm{ent}}(X) = \frac{1}{\theta}\log\left(\mathbb{E}[e^{-\theta X}]\right) = \sup_{Q \in \mathcal{M}_1} \left\{E^Q[-X] -\frac{1}{\theta}H(Q|P)\right\} \,](//upload.wikimedia.org/math/9/3/1/9311aca993b198c9a50df40e097bb0a9.png)
[2]
![\rho^{\mathrm{ent}}(X) = \frac{1}{\theta}\log\left(\mathbb{E}[e^{-\theta X}]\right) = \sup_{Q \in \mathcal{M}_1} \left\{E^Q[-X] -\frac{1}{\theta}H(Q|P)\right\} \,](http://upload.wikimedia.org/math/9/3/1/9311aca993b198c9a50df40e097bb0a9.png)
donde ![H(Q|P) = E\left[\frac{dQ}{dP}\log\frac{dQ}{dP}\right]](http://upload.wikimedia.org/math/1/f/4/1f4f8e1794557fe0e12ed44151b1fbd2.png)
es el entropía relativa de Q << P.[3]
Conjunto de aceptación
El conjunto de aceptación para el riesgo entrópico medida es el conjunto de sobornos con utilidad esperada positiva. Es decir
![A = \{X \in L^p(\mathcal{F}): E[u(X)] \geq 0\} = \{X \in L^p(\mathcal{F}): E\left[e^{-\theta X}\right] \leq 1\}](http://upload.wikimedia.org/math/d/c/4/dc44d3e2dfc0b2c5b9f95b3b74b2c929.png)
donde 
es la función de utilidad exponencial.[3]
Medida del riesgo entrópico dinámico
El medida del riesgo condicional asociados con un riesgo dinámica entrópica con parámetro de aversión al riesgo 
está dada por
![\rho^{\mathrm{ent}}_t(X) = \frac{1}{\theta}\log\left(\mathbb{E}[e^{-\theta X} | \mathcal{F}_t]\right).](http://upload.wikimedia.org/math/b/4/a/b4a8ad9dc97961529edc9ad60d377017.png)
Se trata de un constante de tiempo medida de riesgo si es constante a través del tiempo.[4]
Véase también
- Entrópico valor en riesgo
Referencias
- ^ Rudloff, Birgit; Sass, Jorn; Wunderlich, Ralf (21 de julio de 2008). "Riesgo entrópico limitaciones para la maximización de la utilidad" (pdf). 22 de julio de 2010.
- ^ Föllmer, Hans; Schied, Alexander (2004). Finanzas estocástico: una introducción en tiempo discreto (2 ed.). Walter de Gruyter. p. 174. ISBN978-3-11-018346-7.
- ^ a b Follmer, Hans; Schied, Alexander (08 de octubre de 2008). "Medidas de riesgo coherentes y convexo" (pdf). 22 de julio de 2010.
- ^ Penner, Irina (2007). "Medidas de riesgo dinámico convexo: tiempo de coherencia, prudencia y sostenibilidad" (pdf). 03 de febrero de 2011.