Medida del riesgo dinámico
En matemáticas financieras, un medida del riesgo condicional es un variable aleatoria de la riesgo financiero (particularmente la riesgo) como si se ha medido en algún momento en el futuro. A medida del riesgo puede ser considerado como una medida de riesgo condicional en lo trivial Álgebra Sigma.
A medida del riesgo dinámico es una medida de riesgo que se ocupa de la cuestión de cómo se relacionan las evaluaciones de riesgo en diferentes momentos. Puede ser interpretado como una secuencia de medidas de riesgo condicional. [1]
Contenido
- 1 Medida del riesgo condicional
- 2 Conjunto de aceptación
- 3 Propiedad regular
- 4 Propiedad consistente en tiempo
- 5 Ejemplo: precio superhedging dinámico
- 6 Referencias
Medida del riesgo condicional
Una asignación  es una medida del riesgo condicional si tiene las siguientes propiedades:
es una medida del riesgo condicional si tiene las siguientes propiedades:
- Invariancia condicionadas
-

- Moniticidad
-
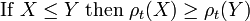
- Normalización
-

Si es un condicional medida del riesgo convexo Entonces también contará con la propiedad:
- Convexidad condicional
-

Un condicional medida de riesgo coherente es una medida de riesgo condicional convexo que además satisface:
- Homogeneidad positiva condicional
-

Conjunto de aceptación
El conjunto de aceptación en el tiempo  asociado con un riesgo condicional medida es
asociado con un riesgo condicional medida es
-
 .
.
Si tienes dada una aceptación listo al tiempo  luego está la correspondiente medida de riesgo condicional
luego está la correspondiente medida de riesgo condicional
donde  es el infimum esencial.[2]
es el infimum esencial.[2]
Propiedad regular
Una medida del riesgo condicional 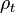 se dice que es regular Si lo haces por cualquier
se dice que es regular Si lo haces por cualquier  y
y  Entonces
Entonces 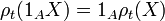 donde
donde  es el función del indicador en
es el función del indicador en  . Cualquier medida normalizada condicional riesgo convexo es regular.[3]
. Cualquier medida normalizada condicional riesgo convexo es regular.[3]
La interpretación de este que el condicional el riesgo en algún nodo futuro (es decir, los Estados financiera ![\rho_t(X)[\omega]](http://upload.wikimedia.org/math/1/1/9/119cd278d2897d8915ef497cd481f9d3.png) ) sólo depende de los posibles estados de ese nodo. En un modelo Binomial Esto sería similar a calcular el riesgo en el subárbol bifurcándose desde el punto de que se trate.
) sólo depende de los posibles estados de ese nodo. En un modelo Binomial Esto sería similar a calcular el riesgo en el subárbol bifurcándose desde el punto de que se trate.
Propiedad consistente en tiempo
Una medida de riesgo dinámico es tiempo coherente si y sólo si  .[4]
.[4]
Ejemplo: precio superhedging dinámico
La dinámica precio superhedging tiene medidas de riesgo condicional de la forma: ![\rho_t(-X) = \operatorname*{ess\sup}_{Q \in EMM} \mathbb{E}^Q[X | \mathcal{F}_t]](http://upload.wikimedia.org/math/3/6/d/36d40967fe5b09cff6ad374b57353895.png) . Es un resultado ampliamente demostrado que esto es también una medida de riesgo constante de tiempo.
. Es un resultado ampliamente demostrado que esto es también una medida de riesgo constante de tiempo.
Referencias
- ^ Acciaio, Beatrice; Penner, Irina (22 de febrero de 2010). "Medidas de riesgo dinámico" (pdf). 22 de julio de 2010.
- ^ Penner, Irina (2007). "Medidas de riesgo dinámico convexo: tiempo de coherencia, prudencia y sostenibilidad" (pdf). 03 de febrero de 2011.
- ^ Detlefsen, K.; Scandolo, G. (2005). "Medidas de riesgo convexo condicional y dinámica". Finanzas y Stochastics 9 (4): 539-561. Doi:10.1007/s00780-005-0159-6.
- ^ Cheridito, Patrick; Stadje, Mitja (octubre de 2008). "Inconsistencia de tiempo del VaR y alternativas consistentes con tiempo".

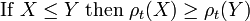



 .
.
