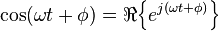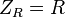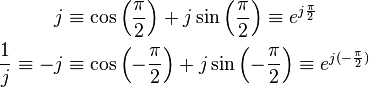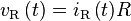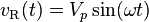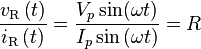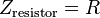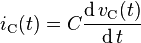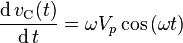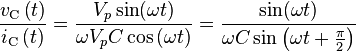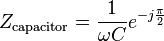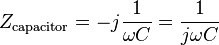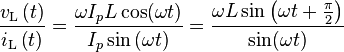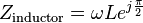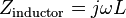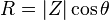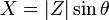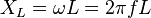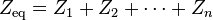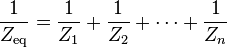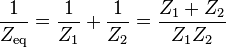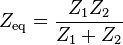Impedancia eléctrica
| Electromagnetismo |
|---|
 |
|
|
Electrostática
|
|
Magnetostática
|
|
Electrodinámica
|
|
Red eléctrica
|
|
Formulación covariante
Tensor electromagnético
(tensor de tensión – energía)
|
|
Científicos
|

Impedancia eléctrica es la medida de la oposición que un circuito presenta a un actual Cuando un voltaje se aplica.
En términos cuantitativos, es el complejo cociente de la tensión de la corriente en un corriente alterna Circuito (AC). Impedancia amplía el concepto de resistencia CA de circuitos y posee tanto la magnitud y fase, a diferencia de la resistencia, que tiene sólo la magnitud. Cuando se conduce un circuito con corriente directa (DC), no hay distinción entre la impedancia y resistencia; este último puede ser pensado como impedancia con cero ángulo de fase.
Es necesario introducir el concepto de impedancia en circuitos de CA porque hay dos mecanismos impiden adicionales que deben tenerse en cuenta además la resistencia normal de circuitos DC: la inducción de voltajes en los conductores autoinducidos por la campos magnéticos de corrientes (inductancia) y el almacenamiento de carga inducida por tensiones entre los conductores (electrostáticocapacitancia). La impedancia causada por estos dos efectos se denomina colectivamente reactancia y forma la imaginario parte de la impedancia compleja considerando formas de resistencia a la real parte.
Suele ser el símbolo de la impedancia Z y se puede representar por escrito su magnitud y fase en forma |Z|∠θ. Sin embargo, la representación de números complejos es a menudo más potente para fines de análisis de circuitos. El término impedancia fue acuñado por Oliver Heaviside en julio de 1886.[1][2] Arthur Kennelly fue el primero en representar la impedancia con números complejos en 1893.[3]
Impedancia se define como el dominio de la frecuencia cociente de la tensión de la corriente.[4] En otras palabras, es el cociente de la tensión – corriente por una sola complejo exponencial en una frecuencia particular ω. En general, la impedancia será un número complejo, con la misma unidades como resistencia, para lo cual el Unidad del SI es el Ohm (Ω). Para una corriente sinusoidal o entrada de voltaje, el forma polar de la impedancia compleja refiere a la amplitud y fase del voltaje y corriente. En particular,
- La magnitud de la impedancia compleja es la relación de la amplitud de la tensión a la amplitud actual.
- La fase de la impedancia compleja es la desplazamiento de fase por el cual la corriente va a la tensión.
El recíproco de impedancia es admisión (es decir, entrada es la relación de corriente a voltaje y convencionalmente lleva unidades de Siemens, antiguamente llamado mutuas).
Contenido
- 1 Impedancia compleja
- 2 La ley de Ohm
- 3 Corriente y voltaje complejo
- 3.1 Validez de la representación compleja
- 3.2 Fasores
- 4 Ejemplos de dispositivos
- 4.1 Derivando las impedancias específica del dispositivo
- 4.1.1 Resistor
- 4.1.2 Condensador
- 4.1.3 Inductor
- 4.1 Derivando las impedancias específica del dispositivo
- 5 Impedancia generalizada de s-avión
- 6 Reactancia vs resistencia
- 6.1 Resistencia
- 6.2 Reactancia
- 6.2.1 Reactancia capacitiva
- 6.2.2 Reactancia inductiva
- 6.2.3 Reactancia total
- 7 Combinar impedancias
- 7.1 Combinación de serie
- 7.2 Combinación paralela
- 8 Medición
- 9 Impedancia variable
- 10 Véase también
- 11 Referencias
- 12 Enlaces externos
Impedancia compleja
Impedancia es representado como un complejo cantidad 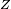 y el término impedancia compleja pueden utilizarse indistintamente; el forma polar captura convenientemente las características de fase y magnitud,
y el término impedancia compleja pueden utilizarse indistintamente; el forma polar captura convenientemente las características de fase y magnitud,
donde la magnitud 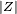 representa la relación de la amplitud de la diferencia de tensión a la amplitud actual, mientras que el argumento
representa la relación de la amplitud de la diferencia de tensión a la amplitud actual, mientras que el argumento 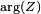 (comúnmente dado el símbolo
(comúnmente dado el símbolo  ) da la diferencia de fase entre voltaje y corriente.
) da la diferencia de fase entre voltaje y corriente.  es el unidad imaginariay se utiliza en lugar de
es el unidad imaginariay se utiliza en lugar de  en este contexto para evitar confusión con el símbolo de corriente eléctrica. En Forma cartesiana,
en este contexto para evitar confusión con el símbolo de corriente eléctrica. En Forma cartesiana,
donde el parte real de la impedancia es la resistencia  y el parte imaginaria es el reactancia
y el parte imaginaria es el reactancia  .
.
Donde es necesario sumar o restar las impedancias la forma cartesiana es más conveniente, pero cuando las cantidades son multiplicadas o divididas el cálculo más simple si se utiliza la forma polar. Un cálculo del circuito, como la búsqueda de la impedancia total de dos impedancias en paralelo, puede requerir la conversión entre formas varias veces durante el cálculo. Conversión entre las formas sigue normal reglas de conversión de números complejos.
La ley de Ohm

 , a través de un carga
, a través de un carga
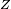 , una corriente de conducción
, una corriente de conducción
 .
.
El significado de impedancia eléctrica puede entenderse sustituyendo en La ley de Ohm.[5][6]
La magnitud de la impedancia 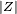 actúa como resistencia, dando la caída de la amplitud de la tensión a través de una impedancia
actúa como resistencia, dando la caída de la amplitud de la tensión a través de una impedancia 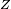 para una determinada corriente
para una determinada corriente  . El factor de fase nos dice que la corriente mantiene la tensión por una fase de
. El factor de fase nos dice que la corriente mantiene la tensión por una fase de 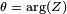 (es decir, en el dominio de tiempo, se desplaza la señal actual
(es decir, en el dominio de tiempo, se desplaza la señal actual 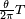 más tarde respecto a la señal de voltaje).
más tarde respecto a la señal de voltaje).
Al igual que la impedancia extiende la ley de Ohm para circuitos de CA, otros resultados de análisis de circuitos DC tales como División de voltaje, División actual, Teorema de Thévenin, y Teorema de Norton puede extenderse también a circuitos de CA mediante la sustitución de resistencia con impedancia.
Corriente y voltaje complejo

Con el fin de simplificar los cálculos, sinusoidal voltaje y corriente ondas comúnmente se representan como funciones con valores de complejo de tiempo denotados como  y
y  .[7][8]
.[7][8]
Impedancia se define como el cociente de estas cantidades.
Sustituye a la ley de Ohm que tenemos
Teniendo en cuenta que esto debe sostener para todos  , nosotros podemos equiparar las magnitudes y fases para obtener
, nosotros podemos equiparar las magnitudes y fases para obtener
La ecuación de la magnitud es la conocida ley del ohmio aplicada el voltaje y la corriente amplitudes, mientras que la segunda ecuación define la relación de fase.
Validez de la representación compleja
Esta representación utilizando exponenciales complejas puede justificarse señalando que (por Fórmula de Euler):
La función sinusoidal valor real representación de voltaje o corriente puede dividirse en dos funciones con valores de complejo. Por el principio de superposición, nosotros podemos analizar el comportamiento de la sinusoide en el lado izquierdo analizando el comportamiento de los dos términos complejos en el lado derecho. Dada la simetría, sólo tenemos que realizar el análisis para un término derecho; los resultados serán idénticos para el otro. Al final de cualquier cálculo, podamos volver a los sinusoides valor real al notar más que
Fasores
Un fasor es un número complejo constante, normalmente expresado en forma exponencial, que representa la amplitud compleja (magnitud y fase) de una función sinusoidal del tiempo. Fasores son utilizados por ingenieros eléctricos para simplificar los cómputos que implican los sinusoides, donde a menudo pueden reducir el problema de una ecuación diferencial a una algebraica.
La impedancia de un elemento del circuito puede definirse como el cociente de la tensión fasor a través del elemento para el fasor corriente a través del elemento, según lo determinado por la relativas amplitudes y fases de la tensión y corriente. Esto es idéntico a la definición de La ley de Ohm mencionados, reconociendo que los factores de 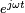 Cancelar.
Cancelar.
Ejemplos de dispositivos

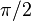 , mientras que el voltaje a través de un inductor
conduce la corriente a través de
, mientras que el voltaje a través de un inductor
conduce la corriente a través de
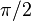 . La tensión idéntica y amplitudes actuales indican que la magnitud de la impedancia es igual a uno.
. La tensión idéntica y amplitudes actuales indican que la magnitud de la impedancia es igual a uno.
La impedancia de un ideal resistor es puramente real y se conoce como un impedancia resistiva:
En este caso, el voltaje y la corriente es proporcionales y en fase.
Ideal inductores y condensadores tienen una puramente imaginario impedancia reactiva:
la impedancia de inductores aumenta con la frecuencia aumenta;
la impedancia de condensadores disminuye a medida que aumenta de frecuencia;
En ambos casos, para una tensión sinusoidal aplicada, la corriente resultante también es sinusoidal, pero en cuadratura, 90 grados fuera de fase con la tensión. Sin embargo, las fases tienen signos opuestos: en un inductor, la corriente es a la zaga; en un condensador la corriente es líder.
Tenga en cuenta las siguientes identidades para la unidad imaginaria y su recíproco:
Por lo tanto el inductor y condensador impedancia ecuaciones pueden ser reescritas en forma polar:
La magnitud da el cambio en la amplitud de la tensión para una amplitud actual dada a través de la impedancia, mientras que los factores exponenciales dan la relación de fase.
Derivando las impedancias específica del dispositivo
Lo que sigue a continuación es una derivación de impedancia para cada uno de los tres básicos circuito elementos: el resistor, el capacitor y el inductor. Aunque la idea puede ser ampliada para definir la relación entre la tensión y corriente de cualquier arbitrario señal, estas derivaciones asumirá sinusoidal señales, puesto que cualquier señal arbitraria se puede aproximar como una suma de sinusoides a través Análisis de Fourier.
Resistor
Para una resistencia, existe la relación:
Se trata de La ley de Ohm.
Teniendo en cuenta que la señal de voltaje
se deduce que
Esto dice que la relación de la amplitud de la tensión AC a corriente alterna Amplitud (AC) a través de un resistor es  , y que el voltaje de CA conduce la corriente a través de un resistor de 0 grados.
, y que el voltaje de CA conduce la corriente a través de un resistor de 0 grados.
Este resultado se expresa comúnmente como
Condensador
Para un condensador, existe la relación:
Teniendo en cuenta que la señal de voltaje
se deduce que
Y así
Esto dice que la relación entre la amplitud de la tensión AC a amplitud de corriente AC a través de un condensador es  y que el voltaje de CA va a la corriente alterna a través de un condensador de 90 grados (o la corriente AC conduce el voltaje de CA a través de un condensador por 90 grados).
y que el voltaje de CA va a la corriente alterna a través de un condensador de 90 grados (o la corriente AC conduce el voltaje de CA a través de un condensador por 90 grados).
Este resultado se expresa comúnmente en forma polar, como
o, aplicando la fórmula de Euler, como
Inductor
Para el inductor, tenemos la relación:
Esta vez, teniendo en cuenta que la señal actual:
se deduce que:
Y así:
Esto dice que es la relación de la amplitud de la tensión AC a amplitud de corriente AC a través de un inductor 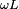 , y que el voltaje de CA conduce la corriente alterna a través de un inductor de 90 grados.
, y que el voltaje de CA conduce la corriente alterna a través de un inductor de 90 grados.
Este resultado se expresa comúnmente en forma polar, como
o, usando la fórmula de Euler, como
Impedancia generalizada de s-avión
Impedancia definida en términos de jω puede estrictamente sólo puede aplicarse a los circuitos que se conducen con una señal AC de estado estacionario. El concepto de impedancia puede extenderse a un circuito energizado con cualquier señal arbitraria utilizando frecuencia complejo En lugar de jω. Complejo frecuencia se da el símbolo s y es, en general, un número complejo. Las señales se expresan en términos de frecuencia complejo tomando el Transformada de Laplace de la dominio de tiempo expresión de la señal. La impedancia de los elementos del circuito básico en esta notación más general es la siguiente:
| Elemento | Expresión de la impedancia |
|---|---|
| Resistor |  |
| Inductor | 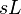 |
| Condensador |  |
Para un circuito de CC esto simplifica a s = 0. Para una señal sinusoidal de AC de estado estacionario s = jω.
Reactancia vs resistencia
Resistencia y reactancia juntos determinan la magnitud y la fase de la impedancia mediante las siguientes relaciones:
En muchas aplicaciones que la fase relativa de la tensión y la corriente no es crítico tan sólo la magnitud de la impedancia es significativa.
Resistencia
Resistencia  es la parte real de la impedancia; un dispositivo con una impedancia puramente resistiva no exhibe ningún desplazamiento de fase entre el voltaje y corriente.
es la parte real de la impedancia; un dispositivo con una impedancia puramente resistiva no exhibe ningún desplazamiento de fase entre el voltaje y corriente.
Reactancia
Reactancia  es la parte imaginaria de la impedancia; un componente con una reactancia finita induce un desplazamiento de fase
es la parte imaginaria de la impedancia; un componente con una reactancia finita induce un desplazamiento de fase  entre el voltaje a través de él y la corriente a través de él.
entre el voltaje a través de él y la corriente a través de él.
Un componente puramente reactivo se distingue por la tensión sinusoidal a través del componente está en cuadratura con la corriente sinusoidal a través del componente. Esto implica que el componente alternativamente absorbe la energía del circuito y luego devuelve energía al circuito. Una reactancia pura no disipará cualquier poder.
Reactancia capacitiva
Un condensador tiene una impedancia puramente reactiva que es inversamente proporcional a la señal frecuencia. Un condensador consiste en dos conductores separados por una aislador, también conocido como un dieléctrico.
En las frecuencias bajas un condensador es circuito abierto, como no hay flujos de carga en el dieléctrico. Provoca una tensión aplicada a través de un condensador carga acumular en un lado; el campo eléctrico debido a la carga acumulada es la fuente de la oposición a la corriente. Cuando el potencial asociado con la carga equilibra exactamente el voltaje aplicado, la corriente va a cero.
Impulsado por una fuente de CA, un condensador acumulará sólo una cantidad limitada de carga antes de que la diferencia de potencial cambia de signo y la carga se disipa. Cuanto mayor sea la frecuencia, la menor carga acumulará y cuanto menor sea la oposición a la corriente.
Reactancia inductiva
Reactancia inductiva 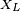 es proporcional a la señal frecuencia
es proporcional a la señal frecuencia  y el inductancia
y el inductancia 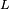 .
.
Un inductor está formado por un conductor en espiral. Ley de Faraday de inducción electromágnetica da la espalda EMF  (voltaje de la corriente de oposición) debido a un tasa de cambio de densidad de flujo magnético
(voltaje de la corriente de oposición) debido a un tasa de cambio de densidad de flujo magnético 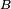 a través de un lazo de corriente.
a través de un lazo de corriente.
Para un inductor que consta de una bobina con  bucles de que este da.
bucles de que este da.
La FCEM es la fuente de la oposición al flujo de corriente. Una constante corriente directa tiene un cero tarifa-de-cambio y ve un inductor como un cortocircuito (está generalmente hecho de un material con un bajo resistividad). Un corriente alterna tiene un promedio de tiempo tarifa-de-cambio que es proporcional a la frecuencia, esto provoca el aumento de la reactancia inductiva con frecuencia.
Reactancia total
La reactancia total está dada por
por lo que es la impedancia total
Combinar impedancias
La impedancia total de muchas redes simples de componentes puede ser calculada usando las reglas para combinar impedancias en serie y paralelo. Las reglas son idénticas a las utilizadas para combinar las resistencias, excepto que los números en general serán números complejos. En la general del caso sin embargo, impedancia equivalente transforma Además de la serie y paralelo será necesarios.
Combinación de serie
Para los componentes conectados en serie, la corriente a través de cada elemento del circuito es el mismo; la impedancia total es la suma de las impedancias del componente.
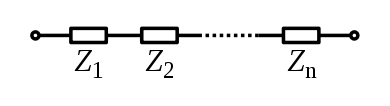
O explícitamente en términos reales e imaginarios:
Combinación paralela
Para los componentes conectados en paralelo, el voltaje en cada elemento del circuito es el mismo; la proporción de las corrientes a través de cualquier dos elementos es el cociente inverso de sus impedancias.
Por lo tanto la inversa impedancia total es la suma de los inversos de las impedancias del componente:
o, cuando n = 2:
La impedancia equivalente  puede ser calculado en términos de la resistencia serie equivalente
puede ser calculado en términos de la resistencia serie equivalente 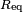 y la reactancia
y la reactancia 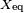 .[9]
.[9]
Medición
La medición de la impedancia de los dispositivos y las líneas de transmisión es un problema práctico en radio tecnología y otros. Pueden llevar a cabo mediciones de impedancia a una frecuencia, o la variación de impedancia del dispositivo en un rango de frecuencias puede ser de su interés. La impedancia puede ser medida o se muestran directamente en ohmios, o pueden aparecer otros valores relacionados con la impedancia; por ejemplo, en un antena de radio el relación de ondas estacionarias o coeficiente de reflexión puede ser más útil que la impedancia sola. Medición de impedancia requiere la medición de la magnitud de voltaje y corriente y la diferencia de fase entre ellos. Impedancia se mide a menudo por métodos de "puente", similar a la corriente continua Puente de Wheatstone; una impedancia de referencia calibrado se ajusta para equilibrar el efecto de la impedancia del dispositivo bajo prueba. Medición de impedancia en dispositivos electrónicos de potencia puede requerir medición simultánea y suministro de energía al dispositivo de funcionamiento.
La impedancia de un dispositivo puede ser calculada por la compleja división del voltaje y la corriente. La impedancia del dispositivo puede calcularse aplicando un voltaje sinusoidal al dispositivo en serie con un resistor, y mida la tensión en la resistencia y a través del dispositivo. Realizar esta medida barriendo las frecuencias de la señal aplicada proporciona la impedancia fase y magnitud.[10]
La utilización de una respuesta de impulso puede utilizarse en combinación con el rápida de Fourier (FFT) para medir rápidamente la impedancia eléctrica de diversos dispositivos eléctricos.[10]
El Medidor de LCR (Inductancia (L), capacitancia (C) y resistencia (R)) es un dispositivo comúnmente usado para medir la inductancia, la resistencia y la capacitancia de un componente; de estos valores se puede calcular la impedancia en cualquier frecuencia.
Impedancia variable
En general, impedancia ni admisión puede ser tiempo variar como son definidos por exponenciales complejas para – ∞ < t < + ∞. Si la relación de tensión – corriente exponencial compleja cambia con el tiempo o amplitud, el elemento del circuito no se puede describir mediante el dominio de la frecuencia. Sin embargo, muchos sistemas (por ejemplo, varicaps que se utilizan en sintonizadores de radio) pueden exhibir las proporciones de tensión – corriente no lineal o variables en el tiempo que parecen ser tiempo-invariante linear (LTI) para las señales pequeñas ventanas de observación; por lo tanto, ellos pueden ser más o menos descritos como teniendo una impedancia varían con el tiempo. Esta descripción es una aproximación; sobre cambios de señal grande o ventanas de observación, la relación de tensión – corriente es no-LTI y no puede ser descrita por impedancia.
Véase también
- Impedancia característica
- Características eléctricas de los altavoces dinámicos
- Alta impedancia
- Immittance
- Puente de impedancia
- Cardiografía
- Impedancias
- Convertidor de impedancia negativa
- Distancia de resistencia
Referencias
- ^ Ciencia, p. 18, 1888
- ^ Oliver Heaviside, El electricista, p. 212, 23 de julio de 1886, reimpreso como Trabajos eléctricos, p 64, librería de AMS, ISBN 0-8218-3465-7
- ^ Kennelly, Arthur. Impedancia (AIEE, 1893)
- ^ Alexander, Charles; Sadiku, Matthew (2006). Fundamentos de circuitos eléctricos (3, revisada ed.). McGraw-Hill. págs. 387-389. ISBN978-0-07-330115-0
- ^ CA la ley de OhmHyperphysics
- ^ Horowitz, Paul; Hill, Winfield (1989). "1". El arte de la electrónica. Cambridge University Press. págs. 32 – 33. ISBN0-521-37095-7.
- ^ Impedancia complejaHyperphysics
- ^ Horowitz, Paul; Hill, Winfield (1989). "1". El arte de la electrónica. Cambridge University Press. págs. 31 – 32. ISBN0-521-37095-7.
- ^ Expresiones de impedanciaHyperphysics
- ^ a b George Lewis Jr., George K. Lewis Sr. y William Olbricht (agosto de 2008). "Rentable banda ancha impedancia eléctrica medición circuito y señal análisis de espectroscopía de piezo-materiales y ultrasonido transductores". Ciencia y tecnología y medición 19 (10): 105102. Bibcode:2008MeScT...19j5102L. Doi:10.1088/0957-0233/19/10/105102. PMC2600501. PMID19081773. de 2008-09-15.
Enlaces externos
- Explicando la impedancia
- Impedancia de la antena
- ECE 209: Revisión de circuitos como sistemas LTI-Breve explicación de análisis de circuito de Laplace-dominio; incluye una definición de impedancia.
|
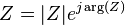

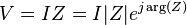

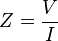
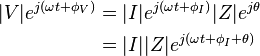

![\ \cos(\omega t + \phi) = \frac{1}{2} \Big[ e^{j(\omega t + \phi)} + e^{-j(\omega t + \phi)}\Big]](http://upload.wikimedia.org/math/3/a/8/3a8a31442a2e1b3eb0c8578b77ec92dd.png)