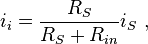Divisor de corriente

Figura 1: Esquema de un circuito eléctrico que ilustran división actual. Notación R_T. se refiere a la total resistencia del circuito a la derecha del resistor R_X.

En electrónica, un divisor de corriente es un simple circuito lineal que produce una salida actual (I_X) es una fracción de su entrada (actualI_T). División actual se refiere a la división de corriente entre las ramas del divisor. Las corrientes en las distintas ramas de tal circuito dividirá siempre de tal manera que se minimice la energía total gastada.

La fórmula que describe un divisor de corriente es similar en forma a la de la divisor de tensión. Sin embargo, la relación que describe la actual división coloca la impedancia de las ramas unconsidered en el numerador, a diferencia de la división de voltaje donde se encuentra la impedancia considerada en el numerador. Esto es porque en divisores de corriente, energía total gastada se reduce al mínimo, dando lugar a las corrientes que van por caminos de menor impedancia, por lo tanto la relación inversa con la impedancia. Por otro lado, divisor de tensión se utiliza para satisfacer Ley de voltaje de Kirchhoff. La tensión alrededor de un lazo necesario sumar hasta cero, así que las caídas de voltaje deben dividirse uniformemente en una relación directa con la impedancia.

Para ser específicos, si dos o más impedancias están en paralelo, se dividirá entre ellos inversamente proporcional a sus impedancias (de acuerdo a la corriente que entra en la combinación La ley de Ohm). Se deduce también que si las impedancias tienen el mismo valor de que la corriente se divide igualmente.

Divisor de corriente

Una fórmula general para la corriente I_X en un resistor R_X está en paralelo con una combinación de otras resistencias de resistencia total R_T es (véase figura 1):

$I_X = \frac{R_T}{(R_X+R_T)}I_T \$

donde I_T la corriente total entra en la red combinada de R_X en paralelo con R_T. Observe que cuando R_T se compone de un combinación paralela de resistencias, decir R₁, R₂, ... etc., entonces debe agregarse el recíproco de cada resistencia para encontrar la resistencia total R_T:

$\frac {1}{R_T} = \frac {1} {R_1} + \frac {1} {R_2} + \frac {1}{R_3} + ... \ .$

Caso general

Aunque el divisor resistivo es más común, el divisor de corriente podrá supeditarse de frecuencia impedancias. En la general del caso la corriente_X viene dada por:

$I_X = \frac{Z_T} {Z_X+Z_T}I_T \ ,$

Uso de admisión

En lugar de utilizar impedancias, la regla actual divisor puede ser aplicada como el divisor de tensión Si la regla admisión se utiliza (el inverso de la impedancia).

$I_X = \frac{Y_X} {Y_{Total}}I_T$

Tenga cuidado de observar Y_Total es una adición simple, no la suma de los inversos invertida (como harías para una red resistiva paralela estándar). Para la figura 1, la corriente_X Sería

$I_X = \frac{Y_X} {Y_{Total}}I_T = \frac{\frac{1}{R_X}} {\frac{1}{R_X} + \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}I_T$

Ejemplo: Combinación RC

Figura 2: Divisor de corriente RC de paso un bajo

La figura 2 muestra un simple divisor actual compuesto por un condensador y un resistor. Usando la fórmula anterior, la corriente en la resistencia viene dada por:

$I_R = \frac {\frac{1}{j \omega C}} {R + \frac{1}{j \omega C} }I_T$

$= \frac {1} {1+j \omega CR} I_T \ ,$

donde Z_C = 1/(jωC) es la impedancia del condensador y j es el unidad imaginaria.

El producto Τ = CR es conocido como el constante de tiempo del circuito y la frecuencia para que ωCR = 1 se llama el frecuencia de la esquina del circuito. Debido a que el condensador tiene cero impedancia a frecuencias altas y la impedancia infinita a bajas frecuencias, la corriente en el resistor se mantiene en su valor de DC I_T para las frecuencias hasta la frecuencia de la esquina, con lo cual cae a cero para frecuencias más altas como el condensador con eficacia cortocircuitos el resistor. En otras palabras, el divisor de corriente es un filtro de paso bajo para la corriente en la resistencia.

Efecto de carga

Figura 3: Un amplificador de corriente (caja gris) impulsado por un (Norton) fuente i_S, R_S) y con una carga de resistencia R_L. Divisor actual en azul caja de entrada) R_S, R_in) reduce la ganancia actual, como lo hace el divisor de corriente en la caja verde en la salida ( R_{hacia fuera}, R_L)

La ganancia de un amplificador generalmente depende de sus origen y carga las terminaciones. Amplificadores de corriente y amplificadores de transconductancia se caracterizan por una condición de salida del cortocircuito, y amplificadores de corriente y amplificadores de transresistance se caracterizan mediante fuentes de corriente ideal impedancia infinita. Cuando un amplificador es terminado por una terminación finita, distinto de cero, o impulsado por una fuente no son ideales, se reduce la ganancia efectiva debido a la efecto de carga a la salida o la entrada, que puede ser entendida en términos de división actual.

La figura 3 muestra un ejemplo de amplificador actual. El amplificador (caja gris) tiene una resistencia de entrada R_in y resistencia de salida R_{hacia fuera} y un aumento de corriente ideal A_i. Con un conductor corriente ideal (resistencia infinita de Norton) toda la fuente actual i_S se convierte en corriente de entrada al amplificador. Sin embargo, para un Controlador de Norton un divisor de corriente está formado en la entrada que reduce la entrada de corriente

$i_{i} = \frac {R_S} {R_S+R_{in}} i_S \ ,$

que es claramente inferior a i_S. Asimismo, por un cortocircuito en la salida, el amplificador proporciona una corriente de salida i_o = A_i i_i para el cortocircuito. Sin embargo, cuando la carga es una resistencia cero R_L, la corriente entregada a la carga es reducida por la división actual en el valor:

$i_L = \frac {R_{out}} {R_{out}+R_{L}} A_i i_{i} \ .$

La combinación de estos resultados, la ganancia actual ideal A_i cuenta con un conductor ideal y un cortocircuito carga se reduce a la aumento de carga A_cargado:

$A_{loaded} =\frac {i_L} {i_S} = \frac {R_S} {R_S+R_{in}}$ $\frac {R_{out}} {R_{out}+R_{L}} A_i \ .$

Las proporciones de resistencia en la expresión anterior se llaman la factores de carga. Para una discusión más de carga en otros tipos de amplificador, vea efecto de carga.

Unilateral versus bilaterales amplificadores

Figura 4: Amplificador actual como una red de dos puertos bilateral; retroalimentación a través de la fuente de voltaje dependiente de ganancia β V/V

Figura 3 y la discusión asociada se refiere a un unilateral amplificador. En un caso más general donde el amplificador está representado por un dos puertos, la resistencia de entrada del amplificador depende de su carga y la resistencia de salida de la impedancia de la fuente. Los factores de carga en estos casos deben emplear las impedancias del amplificador verdadero incluyendo estos efectos bilaterales. Por ejemplo, tomando el amplificador actual unilateral de la figura 3, la red de dos puertos bilateral correspondiente se muestra en la figura 4 basado en h-parámetros. Llevar a cabo el análisis para este circuito, la ganancia actual con retroalimentación A_fb se encuentra

$A_{fb} = \frac {i_L}{i_S} = \frac {A_{loaded}} {1+ {\beta}(R_L/R_S) A_{loaded}} \ .$

Es decir, obtener la corriente ideal A_i se reduce no sólo por los factores de carga, pero debido al carácter bilateral de los dos puertos por un factor adicional (1 + Β (R_L / R_S ) A_cargado ), que es típico de amplificador de retroalimentación negativa circuitos. El factor β (R_L / R_S ) es la actual retroalimentación proporcionada por la fuente de retroalimentación de voltaje del voltaje de ganancia β V/V. Por ejemplo, para una fuente de corriente ideal con R_S = ∞ Ω, la realimentación de tensión no tiene ninguna influencia y para R_L = 0 Ω, no hay tensión de carga, nuevo deshabilitando la retroalimentación.

Véase también

• Divisor de tensión
• Resistor
• La ley de Ohm
• Teorema de Thévenin
• Regulación de voltaje

Enlaces externos

• Universidad de Texas: notas sobre la teoría de circuitos electrónicos

Otras Páginas

• Seguro sin culpa
• Impuestos en la Republica de Irlanda (redireccion de pago relacionados con seguro de Social)
• Recurso compartido
• Amplificacion de polimerasa recombinase
• Publicidad nativa
• Blennidus sanchezi
• Ganancias de tenencia