Cono de solvencia
|
|
Este artículo también puede ser técnica para la mayoría de los lectores a entender. (Diciembre de 2013) |
El cono de solvencia es un concepto utilizado en matemáticas financieras que modela las posibles operaciones en el mercado financiero. Esto es de particular interés para los mercados con costos de transacción. En concreto, es el cono convexo de las carteras pueden intercambiarse a las carteras de los componentes no negativo (incluido el pago de los gastos de transacción).
Contenido
- 1 Matemáticamente
- 1.1 Definición
- 2 Usos
- 3 Ejemplos
- 3.1 Mercado sin fricción
- 3.2 Con los costos de transacción
- 4 Notas
- 5 Referencias
Matemáticamente
Si se les da un matriz de oferta-demanda 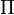 para
para  los activos que
los activos que  y
y  es el número de activos que con cualquier cantidad no negativos de ellos pueden ser "desechados" (tradicionalmente
es el número de activos que con cualquier cantidad no negativos de ellos pueden ser "desechados" (tradicionalmente 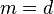 ). Entonces el cono de solvencia
). Entonces el cono de solvencia  es el cono convexo atravesado por los vectores de la unidad
es el cono convexo atravesado por los vectores de la unidad  y los vectores
y los vectores  .[1]
.[1]
Definición
Un cono de solvencia  nada está cerrado cono convexo tal que
nada está cerrado cono convexo tal que  y
y  .[2]
.[2]
Usos
Un proceso de conos de solvencia (al azar)  es un modelo de un mercado financiero. Esto a veces se llama un proceso de mercado.
es un modelo de un mercado financiero. Esto a veces se llama un proceso de mercado.
La negativa de un cono de solvencia es el conjunto de carteras que pueden obtenerse a partir de la cartera de cero. Esto está íntimamente relacionada con carpetas de autofinanciación.[citación necesitada]
El doble cono de la solvencia del cono) ) es el conjunto de precios que definiría una menos fricción sistema para los activos que es consistente con el mercado de precios. Esto también se llama un sistema de precios constante.[1]
) es el conjunto de precios que definiría una menos fricción sistema para los activos que es consistente con el mercado de precios. Esto también se llama un sistema de precios constante.[1]
Ejemplos


Asumir que hay 2 activos, A y M con 1 a 1 intercambio posible.
Mercado sin fricción
En un mercado sin fricción, obviamente podemos hacer (1A, M-1) y (-1A, 1 M) en carteras no negativos, por lo tanto  . Tenga en cuenta que (1,1) es el "vector de precios".
. Tenga en cuenta que (1,1) es el "vector de precios".
Con los costos de transacción
Además asume que hay un 50% los costos de transacción para cada negocio. Esto significa que (1A, M-1) y (-1A, 1 M) no pueden ser intercambiados en carpetas no negativo. Pero, (2A, M-1) y (-1A, 2 M) pueden ser negociados en carteras no negativo. Puede verse que  .
.
El cono doble de los precios así es más fácil de ver en términos de precios de la A en términos de M (y similar hecho por precio de M en términos de A):
- alguien le ofrece 1A para tM:
 por lo tanto hay arbitraje si
por lo tanto hay arbitraje si 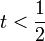
- alguien le ofrece tM para 1A:
 por lo tanto hay arbitraje si
por lo tanto hay arbitraje si 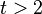
Notas
Si un cono de solvencia  :
:
- contiene una línea, entonces no hay un cambio posible sin los costos de transacción.
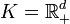 , entonces no hay ningún intercambio posible, es decir, el mercado está totalmente ilíquidos.
, entonces no hay ningún intercambio posible, es decir, el mercado está totalmente ilíquidos.
Referencias
- ^ a b Schachermayer, Walter (15 de noviembre de 2002). "El teorema Fundamental de Asset Pricing debajo de los costos de transacción proporcional en tiempo discreto finito".
- ^ Hamel, A. H.; Heyde, f el. (2010). "Dualidad por valor conjunto de medidas de riesgo" (pdf). SIAM Journal on matemáticas financieras 1 (1): 66 – 95. Doi:10.1137/080743494. 17 de agosto de 2012.
 por lo tanto hay arbitraje si
por lo tanto hay arbitraje si 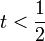
 por lo tanto hay arbitraje si
por lo tanto hay arbitraje si 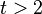
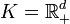 , entonces no hay ningún intercambio posible, es decir, el mercado está totalmente ilíquidos.
, entonces no hay ningún intercambio posible, es decir, el mercado está totalmente ilíquidos.