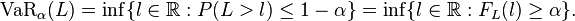Valor en riesgo
- Fue vuelve a dirigir aquí. Para la técnica estadística VAR, ver Vectores autorregresivos. Para la estadística denotaba Var o var, ver Varianza.

En matemáticas financieras y gestión del riesgo financiero, valor en riesgo (Fue) es un ampliamente utilizado medida del riesgo de la riesgo de pérdida en un específico cartera de los activos financieros. Para una cartera determinada, horizonte de tiempo, y probabilidad p, el 100p% VaR se define como un valor umbral de pérdida, tal que la probabilidad de que la pérdida de la cartera en el horizonte de tiempo dado excede este valor es p. Esto supone Mark-to-market precios, mercados normales y no en la cartera de comercio.[1]
Por ejemplo, si una cartera de acciones tiene un día 5% VaR de $ 1 millón, hay una probabilidad de 0.05 que el portafolio caerá en valor por más de $ 1 millón durante un período de un día si no hay ninguna negociación. Informalmente, una pérdida de $ 1 millón o más en esta cartera se espera 1 día por 20 días (debido a la probabilidad de 5%). Una pérdida que supere el umbral de VaR se denomina una "rotura de VaR".[2]
VaR tiene cuatro usos principales Finanzas: gestión del riesgo, financieros control, Presentación de informes financieros y computación capital regulatorio. VaR a veces se utiliza en aplicaciones no financieras.[3]
Importantes ideas relacionadas son capital económico, backtesting, prueba de esfuerzo, déficit esperado, y expectativa condicional cola.[4]
Contenido
- 1 Detalles
- 2 Variedades de VaR
- 2.1 VaR en la gobernanza
- 3 Definición matemática
- 4 Medida del riesgo y métricas de riesgo
- 5 Gestión del riesgo VaR
- 6 Métodos de cálculo
- 7 Historia de VaR
- 8 Crítica
- 8.1 VaR, CVaR y EVaR
- 9 Véase también
- 10 Referencias
- 11 Enlaces externos
Detalles
Parámetros comunes para VaR son las probabilidades de 1% y 5% y un día y semana dos horizontes, aunque otras combinaciones están en uso.[5]
La razón para asumir los mercados normales y no comerciales y a limitar la pérdida de las cosas que se mide en cuentas diarias, es hacer que la pérdida observable. En algunos eventos financieras extremas puede ser imposible determinar las pérdidas, porque los precios del mercado no están disponibles o porque rompe la institución de pérdida de carga. Algunas de las consecuencias a largo plazo de los desastres, tales como demandas, pérdida de mercado confianza y empleado de la moral y la debilitación de marcas pueden tomar mucho tiempo para jugar y pueden ser difíciles asignar entre decisiones específicas previas. VaR marca el límite entre días normales y los eventos extremos. Las instituciones pueden perder mucho más que la cantidad de VaR; todo lo que puede decirse es que no lo harán muy a menudo.[6]
El nivel de probabilidad y es igualmente a menudo especificado como uno menos la probabilidad de un descanso de VaR, para que el VaR en el ejemplo anterior sería llamado un día 95% VaR en lugar de un día 5% var. Esto generalmente no lleva a confusión porque la probabilidad de VaR se rompe casi siempre es pequeña, ciertamente menos de 0.5.[1]
Aunque casi siempre representa una pérdida, VaR convencionalmente se informa como un número positivo. Un VaR negativo implicaría que la cartera tiene una alta probabilidad de obtener una ganancia, por ejemplo un día 5% VaR de negativo $ 1 millón implica que el portafolio tiene un 95% de posibilidades de hacer más de $ 1 millón en el día siguiente.[7]
Otra incongruencia es que VaR es a veces para referirse a ganancias y pérdidas al final del período y a veces como la pérdida máxima en cualquier momento durante el período. La definición original era el último, pero en la década de 1990 cuando se agrega VaR a través de operaciones con escritorios y zonas horarias, valoración final del día fue el número sólo confiable el anterior se convirtió en el de facto definición. Como la gente comenzó a usar VaRs varios días en la segunda mitad del decenio de 1990, casi siempre se estimó la distribución al final del periodo sólo. También es teóricamente más fácil tratar con una estimación puntual en comparación con un máximo en un intervalo. Por lo tanto la definición final del período es la más común tanto en la teoría y la práctica de hoy.[8]
Variedades de VaR
La definición de VaR nonconstructive; especifica un propiedad VaR debe tener, pero no se como calcular el var. Además, hay un amplio alcance para la interpretación de la definición.[9] Esto ha llevado a dos tipos generales de VaR, utilizado principalmente en gestión del riesgo y el otro principalmente para la medición del riesgo. La distinción no es sostenida, sin embargo, y las versiones híbridas se utilizan típicamente en financiera control, Presentación de informes financieros y computación capital regulatorio.[10]
A un administrador de riesgo, VaR es un sistema, no es un número. El sistema se ejecuta periódicamente (generalmente diaria) y el número publicado es comparado con el movimiento de precios computada en la apertura de posiciones sobre el horizonte de tiempo. Nunca hay cualquier ajuste posterior a la VaR publicado, y no hay distinción entre VaR roturas causadas por errores de entrada (incluyendo Tecnología de la información averías, fraude y Rogue trading), errores de cálculo (incluyendo incapacidad para producir un VaR a tiempo) y los movimientos del mercado.[11]
A frecuentista se realiza el reclamo, que la frecuencia de roturas de VaR a largo plazo será igual a la probabilidad especificada, dentro de los límites de error de muestreo, y que será el VaR se rompe independiente en el tiempo y independiente el nivel de var. Esta afirmación es validada por un backtest, una comparación de VaRs publicados a los movimientos del precio real. En esta interpretación, muchos sistemas diferentes pueden producir VaRs con igual de buena backtest, pero amplio desacuerdos en valores diarios VaR.[1]
Para la medición del riesgo que es necesario un número, no un sistema. A Probabilidad bayesiana se realiza el reclamo, que dada la información y las creencias en el tiempo, la probabilidad subjetiva de un VaR descanso era el nivel especificado. VaR se ajusta después de los hechos para corregir errores en insumos y computación, pero no para incorporar información disponible en el momento de cómputo.[7] En este contexto "backtest"tiene un significado diferente. En lugar de comparar VaRs publicados a los movimientos del mercado real durante el período de tiempo que el sistema ha estado en operación, VaR retroactivo es computado de fregado datos sobre como un período de tiempo como los datos están disponibles y considere pertinente. Los mismos datos de posición y los precios de los modelos se utilizan para calcular el VaR como determinar los movimientos de precio.[2]
Aunque algunas de las fuentes enumeran aquí tratan solamente una clase de VaR como legítimo, la mayoría de los recientes parece estar de acuerdo la gestión del riesgo que var es superior para la toma de decisiones a corto plazo y tácticas hoy, mientras que la medición del riesgo que var debe utilizarse para comprender el pasado y hacer a mediano plazo y las decisiones estratégicas para el futuro. Cuando VaR se utiliza para control financiero o Presentación de informes financieros deben incorporar elementos de ambos. Por ejemplo, si un trading desk se lleva a cabo a un límite de VaR, que es tanto una regla de gestión de riesgos para decidir qué riesgos para permitir que hoy en día, y una entrada en el cómputo de medición de riesgo de la de escritorio ajustada al riesgo retorno al final del período de notificación.[4]
VaR en la gobernanza
VaR puede aplicarse también a la gobernabilidad de las dotaciones, fideicomisos y los planes de pensiones. Esencialmente Síndicos adoptan métricas de valores en riesgo cartera para toda la cuenta combinada y las partes diversificadas administradas individualmente. En lugar de las estimaciones de probabilidad simplemente definen los niveles máximos de pérdida aceptable para cada uno. Hacerlo proporciona una métrica fácil para supervisión y agrega responsabilidad como gerentes entonces se dirigen a manejar, pero con la restricción adicional para evitar las pérdidas dentro de un parámetro de riesgo definido. VaR utilizada de esta manera suma relevancia, así como una manera fácil de supervisar el control de medición de riesgos mucho más intuitivo que la desviación estándar del retorno. Uso de VaR en este contexto, así como una crítica que valga la pena a bordo de las prácticas de gobierno en lo que atañe a la supervisión de la gestión de inversiones en general puede encontrarse en Mejores prácticas en el gobierno.[12]
Definición matemática
Dado un nivel de confianza 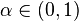 , el VaR de la cartera en el nivel de confianza
, el VaR de la cartera en el nivel de confianza  está dado por el número más pequeño
está dado por el número más pequeño  tal que la probabilidad de que la pérdida
tal que la probabilidad de que la pérdida  excede
excede  es en la mayoría
es en la mayoría 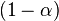 .[3] Matemáticamente, si
.[3] Matemáticamente, si  es la pérdida de una cartera, entonces
es la pérdida de una cartera, entonces  es el nivel
es el nivel  -cuantil, es decir,
-cuantil, es decir,
-
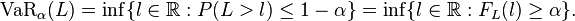 [13]
[13]
La igualdad de la izquierda es una definición de var. La igualdad de derecha asume una distribución de probabilidad subyacente, que hace verdadero sólo para riesgo de var paramétrico gerentes suelen asuman que una fracción de los malos eventos habrá indefinido las pérdidas, porque los mercados están cerrados o liquidez, o porque la entidad teniendo la pérdida rompe o pierde la capacidad de calcular las cuentas. Por lo tanto, no aceptan los resultados basados en el supuesto de una distribución de probabilidad definida.[6] Nassim Taleb ha calificado esta hipótesis, "charlatanería".[14] Por otro lado, muchos académicos prefieren asumir una distribución bien definida, aunque generalmente con colas gordas.[1] Este punto ha causado probablemente más contención entre VaR teóricos que cualquier otro.[9]
Valor de riesgos también puede escribirse como una medida del riesgo de distorsión otorgado por la función de distorsión  [15][16]
[15][16]
Medida del riesgo y métricas de riesgo
El término "VaR" es utilizado tanto para un riesgo medida y un métricas de riesgo. Esto conduce a veces a la confusión. Las fuentes antes de 1995 generalmente enfatizan la medida del riesgo, fuentes posteriores están más probables que enfatizan la métrica.
La medida del riesgo VaR define riesgo como Mark-to-market pérdida de una cartera fija sobre un horizonte de tiempo fijo, suponiendo que los mercados normales. Hay muchas medidas alternativas de riesgo en las finanzas. En lugar de mark-to-market, que utiliza los precios de mercado para definir la pérdida, pérdida a menudo se define como cambio en valor fundamental. Por ejemplo, si una institución tiene un préstamo declina en precio de mercado porque interés las tasas suben, pero no tiene ningún cambio en los flujos de efectivo o la calidad de crédito, algunos sistemas no reconoce una pérdida. O podríamos tratar de incorporar la económico costo de las cosas no se mide en diario Estados financieros, tales como la pérdida de confianza de los mercados o la moral del empleado, deterioro del valor de las marcas o demandas.[4]
En lugar de asumir una cartera fija sobre un horizonte de tiempo fijo, algunas medidas de riesgo incorporan el efecto de comercio esperada (tales como un orden de stop loss) y tener en cuenta el período de tenencia esperada de las posiciones. Por último, algunas medidas de riesgo ajustan para los posibles efectos de los mercados anormales, en lugar de excluirlos de la computación.[4]
La métrica de riesgo VaR resume la distribución de posibles pérdidas por un cuantil, un punto con una determinada probabilidad de pérdidas mayores. Métricas alternativas comunes son desviación estándar, es decir desviación absoluta, déficit esperado y riesgo.[1]
Gestión del riesgo VaR
Los partidarios de la gestión de riesgos basado en VaR reclaman el primero y posiblemente mayor beneficio de VaR es la mejora en sistemas y lo modelado obliga a una institución. En 1997, Philippe Jorion escribió:[17]
[T] él mayor beneficio de VAR radica en la imposición de una metodología estructurada para pensar críticamente sobre el riesgo. Instituciones que pasan por el proceso de la informática su VAR fuerzan para afrontar su exposición a riesgos financieros y establecer una función de gestión de riesgo apropiada. Así el proceso de llegar a VAR puede ser tan importante como el número de sí mismo.
Publican varios diarios, puntual y con especificado Estadística propiedades sostiene cada parte de una organización comercial a un objetivo de alto estándar. Robustos sistemas de backup y por defecto supuestos deben ser aplicados. Posiciones que son registradas, modeladas o incorrectamente el precio destacan, como fuentes de datos que son inexactos o tardía y sistemas que son con demasiada frecuencia hacia abajo. Todo lo que afecta a pérdidas y ganancias que queda fuera de otros informes se mostrará en VaR inflado o VaR excesivo rompe. "Una institución toma de riesgos que No lo hace calcular el VaR puede escapar el desastre, sino una institución que No se puede calcular el que var no lo hará". [18]
El segundo afirmó beneficio del VaR es que separa riesgo en dos regímenes. Dentro del límite de VaR, convencional Estadística los métodos son fiables. Datos relativamente a corto plazo y específicos pueden utilizarse para el análisis. Las estimaciones de la probabilidad son significativas, porque hay datos suficientes para ponerlos a prueba. En cierto sentido, no existe cierto riesgo porque tienes una suma de muchos independiente observaciones con una izquierda limitados en el resultado. Un casino no le preocupa ya sea rojo o negro se le ocurrirá en la próxima vuelta de ruleta. Los administradores de riesgos alentar riesgo productivo en este régimen, porque hay un cierto costo. La gente tiende a preocuparse demasiado por estos riesgos, porque ocurren con frecuencia, y no lo suficiente sobre lo que podría ocurrir en los peores días.[19]
Fuera del límite de VaR, todas las apuestas están fuera. Riesgo debe ser analizado con prueba de esfuerzo basado en datos de mercado amplio y a largo plazo.[20] Las declaraciones de probabilidad ya no son significativas.[21] Conocer la distribución de las pérdidas más allá de la VaR punto es tanto imposible e inútil. El Gerente de riesgo debería concentrarse en cambio en asegurándose de que son buenos planes en lugar de limitar la pérdida si es posible y para sobrevivir a la pérdida si no es así.[1]
Un sistema específico utiliza tres regímenes.[22]
- VaR de una a tres veces son ocurrencias normales. Esperas descansos periódicos de VaR. Por lo general tiene la distribución de pérdida colas gordas, y se puede meter más de una oportunidad en un corto periodo de tiempo. Además, los mercados pueden ser anormales y comercio puede exacerbar las pérdidas, y puede tomar las pérdidas que no se mide en diario marcas tales como demandas, pérdida de confianza de la moral y el mercado de empleados y la debilitación de las marcas. Para que una institución que no puede lidiar con las pérdidas de VaR tres veces como rutinarios acontecimientos probablemente no sobrevivirá el tiempo suficiente para establecer un sistema de VaR.
- Tres a diez veces VaR es la gama de prueba de esfuerzo. Las instituciones deben tener la seguridad que han examinado todos los acontecimientos previsibles que causarán pérdidas en esta gama y están preparados para sobrevivir a ellas. Estos eventos son demasiado raros para estimar las probabilidades confiablemente, así que los cálculos de riesgo/rendimiento son inútiles.
- Eventos previsibles no deberían causar pérdidas más allá de diez veces var. Si lo hacen deben ser cubiertos asegurado, o el plan de negocios debe cambiarse para evitarlos o VaR debe ser aumentada. Es difícil hacer negocios si pérdidas previsibles son órdenes de magnitud más grandes que las pérdidas diarias muy grandes. Es difícil planear para estos eventos, porque están fuera de escala con la experiencia cotidiana. Por supuesto habrá pérdidas imprevisibles VaR más de diez veces, pero es inútil preverlas, no sabes mucho sobre ellas y resulta innecesario preocuparse. Mejor esperar que la disciplina de la preparación para todos previsibles tres a diez veces las pérdidas VaR mejorará posibilidades para sobrevivir a las pérdidas imprevistas y más grandes que inevitablemente se producen.
"Un gerente de riesgo tiene dos trabajos: hacer que la gente tome más riesgo el 99% del tiempo que es seguro hacerlo, y sobrevivir el otro 1% del tiempo. VaR es la frontera".[18]
Métodos de cálculo
VaR puede ser estimado o paramétrica (por ejemplo, varianza-covarianza VaR o Delta-gamma VaR) o paramétrica (por ejemplo, histórico simulación VaR o muestrear VaR).[4][6] Métodos no paramétricos de estimación del VaR se discuten en Markovich [23] y Novak.[24]
Un informe de McKinsey[25] Publicado en puede 2012 estima que 85% de los grandes bancos utilizaban simulación histórica. El otro 15% utiliza métodos de Monte Carlo.
Historia de VaR
El problema de la medición del riesgo es una vieja en estadísticas, economía y Finanzas. Gestión del riesgo financiero ha sido una preocupación de los reguladores y ejecutivos financieros durante mucho tiempo así. Análisis retrospectivo ha encontrado algunos conceptos VaR-como en esta historia. Pero VaR no surgió como un concepto distinto hasta finales de los ochenta. El evento desencadenante fue el mercado de valores El Crash de 1987. Esta fue la primera crisis financiera importante en el cual mucho de formados académicamente quants estaban en alto bastantes posiciones que preocuparse por la supervivencia de toda la empresa.[1]
El choque fue tan improbable dado estándar Estadística modelos, que se llama la base entera de Quant Finanzas en entredicho. Una reconsideración de la historia llevado algunos quants decidir hubo crisis recurrentes, sobre uno o dos por cada década, que embarga a los supuestos estadísticos incrustados en los modelos utilizados para Trading, gestión de inversiones y derivado de la fijación de precios. Estos afectaron muchos mercados al mismo tiempo, los que no eran generalmente incluyendo correlacionados, y rara vez causa económica discernible o advertencia (aunque eran abundantes explicaciones después de los hechos).[21] Mucho más tarde, fueron nombrados"Cisnes negros"por Nassim Taleb y el concepto extendido mucho más allá de Finanzas.[26]
Si estos eventos fueron incluidos en Análisis cuantitativo ellos dominaron resultados y condujeron a estrategias que no funcionaba día a día. Si estos eventos fueron excluidos, los beneficios obtenidos entre "Cisnes negros" podrían ser mucho menores que las pérdidas sufridas en la crisis. Las instituciones podrían fallar como resultado.[18][21][26]
VaR fue desarrollado como una manera sistemática para segregar eventos extremos, que son estudiados cualitativo sobre historia a largo plazo y los acontecimientos de mercado amplio, desde los movimientos de precios todos los días, que son estudiados cuantitativamente utilizando datos a corto plazo en mercados específicos. Se esperaba que "Cisnes negros" sería precedidos por aumentos en VaR Estimado o aumento de la frecuencia de roturas de VaR, en por lo menos algunos mercados. La medida en que esta ha demostrado para ser verdad es controvertida.[21]
Los mercados anormales y el comercio fueron excluidos de la estimación del VaR para hacerla observables.[19] No siempre es posible definir la pérdida si, por ejemplo, los mercados están cerrados como después 9/11, o severamente ilíquidos, como ocurrió varias veces en 2008.[18] Las pérdidas también pueden ser difíciles de definir si la institución asumir riesgos falla o se rompe.[19] Una medida que depende de proveedores tomando ciertas acciones y evitar otras acciones, puede llevar a Referencia del uno mismo.[1]
Esta es la gestión de riesgos var. Fue establecido en Comercio cuantitativa grupos en varias instituciones financieras, en particular Bankers Trust, antes de 1990, aunque ni el nombre ni la definición había sido estandardizada. No había ningún esfuerzo para VaRs agregadas a través de mesas de negociación.[21]
Los acontecimientos financieros de principios de los noventa encontraron muchas firmas en problemas porque la misma apuesta subyacente se hicieron en muchos lugares en la firma, en formas no evidente. Puesto que muchos escritorios comerciales ya computan VaR la gestión de riesgos, y era la medida del riesgo sólo comunes que podría ser tanto definida para todas las empresas y agregada sin fuertes presunciones, fue la elección natural para reportar firmwide riesgo. J. P. Morgan CEO Dennis Weatherstone famosa frase pidió un "4:15 informe" que combina toda firma riesgo en una sola página, disponible en 15 minutos cerca del mercado.[9]
El riesgo de medición que var fue desarrollado para este propósito. Era más extenso en el desarrollo J. P. Morgan, que publicó la metodología y dio acceso libre a las estimaciones de los parámetros necesarios subyacentes en 1994. Esta fue la primera vez VaR había sido expuesto más allá de un grupo relativamente pequeño de quants. Dos años más tarde, la metodología fue desprendida en parte ahora negocio con fines de lucro independiente de RiskMetrics Group.[9]
En 1997, la US Securities and Exchange Commission dictaminó que las corporaciones públicas debe revelar información cuantitativa sobre su derivados actividad. Principales bancos y distribuidores decidieron implementar la regla incluyendo VaR información en las notas a su Estados financieros.[1]
Adopción en el mundo de la Acuerdo de Basilea II, a partir de 1999 y a punto de finalizar hoy, le dio más impulso al uso de var VaR es el recomendado: medida de riesgo de mercado, y se utilizan conceptos similares a VaR en otras partes del acuerdo.[1]
Crítica
VaR ha sido controversial desde que se mudó de trading escritorios en el ojo público en 1994. Un famoso 1997 debate entre Nassim Taleb y Philippe Jorion figuran algunos de los principales puntos de discordia. Taleb afirmó VaR:[27]
- Ignorado de 2.500 años de experiencia a favor no probados modelos construidos por los comerciantes no
- Era charlatanería porque alegó estimar los riesgos de acontecimientos raros, lo cual es imposible
- Dio la falsa confianza
- Podría ser explotado por los comerciantes
En 2008 David Einhorn y Aaron Brown VaR debatido en Revisión de asociación global de riesgos profesionales[18][28] Einhorn comparado VaR con "un airbag que trabaja todo el tiempo, excepto cuando tienes un accidente". Más que cobró VaR:
- Condujo a la excesiva toma de riesgos y el apalancamiento de las instituciones financieras
- Centrado en los riesgos manejables cerca del centro de la distribución y omite las colas
- Crea un incentivo para tomar "excesiva pero los riesgos remotos"
- Era "potencialmente catastrófica cuando su uso crea una falsa sensación de seguridad entre altos ejecutivos y organismos de control."
New York Times reportero Joe Nocera escribió una extensa obra Mala gestión del riesgo[29] en 04 de enero de 2009 discutiendo la función VaR jugó en el Crisis financiera de 2007-2008. Tras entrevistar a los administradores de riesgos (incluyendo varios de los citados) el artículo sugiere que VaR era muy útil para los expertos en riesgos, pero sin embargo exacerbaron la crisis dando seguridad falsa a los reguladores y los ejecutivos del banco. Una poderosa herramienta para los administradores de riesgos profesionales, VaR es retratado como fácil malinterpretar y peligroso cuando incomprendido.
Taleb, en 2009, declaró en el Congreso pidiendo la prohibición de VaR en dos argumentos, el primero que "los riesgos de la cola son no medibles" científicamente y la segunda es que para anclaje razones de VaR para conducir a la toma de riesgos más altos.[30]
Una queja común entre los académicos que VaR no es subadditive.[4] Eso significa que el VaR de una cartera combinada puede ser mayor que la suma de las VaRs de sus componentes. A un administrador de riesgo practicar esto tiene sentido. Por ejemplo, la sucursal del Banco promedio en los Estados Unidos es robada cada diez años. Una sola sucursal tiene cerca de 0,0004% posibilidades de ser robado en un día específico, así que el riesgo de robo no pensaría en un día 1% var. No ni siquiera sería dentro de un orden de magnitud de que así es en la gama donde la institución debe no te preocupes, debe asegurar contra él y seguir los consejos de los aseguradores de precauciones. El asunto del seguro es a riesgos globales que están más allá de los límites individuales de VaR y llevarlos a una cartera lo suficientemente grande como para obtener estadística previsibilidad. No rentable para que un banco de una rama a un experto en seguridad personal.
Como las instituciones más ramas, el riesgo de un robo en un día específico se eleva a dentro de un orden de magnitud de var. En ese punto tiene sentido para hacer pruebas de estrés internas y analizar el riesgo propio de la institución. Gastará menos seguro y más de experiencia interna. Para una institución bancaria muy grande, robos son una ocurrencia diaria rutina. Las pérdidas son parte del cálculo del VaR diario y seguimiento estadístico en lugar de caso por caso. Un departamento de seguridad interna considerable se encarga de la prevención y control, el gerente general de riesgos sólo rastrea la pérdida como cualquier otro costo de hacer negocios.
Como carteras o instituciones más grandes, riesgos específicos cambian de baja-probabilidad/bajo-previsibilidad/alto impacto estadísticamente previsibles pérdidas de bajo impacto individual. Que los medios se mueven de la gama del exterior lejano VaR, a ser asegurados, a cerca de VaR exterior, para ser analizadas caso por caso, para dentro de VaR, a ser tratadas estadísticamente.[18]
Incluso los partidarios de VaR generalmente están de acuerdo hay abusos comunes de VaR:[6][9]
- Refiriéndose a VaR como un "peor" o "máxima tolerable" pérdida. De hecho, esperar dos o tres pérdidas anuales que exceden el día 1% var.
- Haciendo VaR reducción o control VaR la preocupación central de gestión de riesgos. Es mucho más importante preocuparse de lo que sucede cuando las pérdidas superan var.
- Asumiendo las pérdidas plausibles será menor que algunos múltiples, a menudo tres, de var. El punto entero de VaR es que las pérdidas pueden ser extremadamente grandes y a veces imposible de definir, una vez que llegues más allá del punto de VaR. A un administrador de riesgo, VaR es el nivel de pérdidas a que dejas de tratar de adivinar lo que sucederá después y comenzar a prepararse para cualquier cosa.
- Reportando un VaR que no ha pasado un backtest. Independientemente de cómo se calcula el VaR, debería haber producido el número correcto de roturas (dentro de error de muestreo) en el pasado. Una violación específica común de esto es dar un VaR basado en la suposición no verificada que todo sigue un distribución normal multivariante.
VaR, CVaR y EVaR
El VaR no es una medida de riesgo coherente puesto que viola la propiedad sub-aditividad, que es

Sin embargo, puede ser limitada por medidas de riesgo coherentes como Valor en riesgo condicional (CVaR) o entrópico valor en riesgo (EVaR). De hecho, para  (con
(con  el conjunto de todos Borel funciones medibles cuyo Función generadora de momento existe para todos los valores reales positivos) tenemos
el conjunto de todos Borel funciones medibles cuyo Función generadora de momento existe para todos los valores reales positivos) tenemos

donde

en el cual  es la función generadora de momento de
es la función generadora de momento de  en
en  . En las ecuaciones anteriores la variable
. En las ecuaciones anteriores la variable  denota la pérdida financiera, en lugar de riqueza como suele ser el caso.
denota la pérdida financiera, en lugar de riqueza como suele ser el caso.
Véase también
- Directiva de suficiencia de capital
- Riesgo de valuación
- Valor en riesgo condicional
- Entrópico valor en riesgo
- Riesgo relativo retorno
Referencias
- ^ a b c d e f g h i j Jorion, Philippe (2006). Valor en riesgo: el nuevo punto de referencia para la gestión de riesgos financieros (3ª ed.). McGraw-Hill. ISBN978-0-07-146495-6.
- ^ a b Holton, Glyn A. (2014). Value-at-Risk: Teoría y práctica segunda edición, e-book.
- ^ a b McNeil, Alexander; Frey, Rüdiger; Embrechts, Paul (2005). Gestión de riesgos cuantitativa: Conceptos técnicas y herramientas. Princeton University Press. ISBN978-0-691-12255-7.
- ^ a b c d e f Dowd, Kevin (2005). Medición de riesgo de mercado. John Wiley & Sons. ISBN978-0-470-01303-8.
- ^ Pearson, Neil (2002). Riesgo presupuesto: Cartera para solucionar problemas con Value-at-Risk. John Wiley & Sons. ISBN978-0-471-40556-6.
- ^ a b c d Aaron Brown (Marzo de 2004), La insoportable levedad del riesgo de mercado cruzadoWilmott revista
- ^ a b Crouhy, Michel; Galai, Dan; Mark, Robert (2001). Lo esencial de la gestión del riesgo. McGraw-Hill. ISBN978-0-07-142966-5.
- ^ Jose A. Lopez (septiembre de 1996). "Evaluación reguladora de modelos de valor en riesgo". Wharton centro financiero de las instituciones trabajando papel 96-51.
- ^ a b c d e Kolman, Joe; Onak, Michael; Jorion, Philippe; Taleb, Nassim; Derman, Emanuel; Putnam, Blu; Sandor, Richard; Jonas, Stan; Dembo, Ron; Holt, George; Tanenbaum, Richard; Margrabe, William; Mudge, Dan; Lam, James; Rozsypal, Jim (abril de 1998). "Mesa redonda: los límites del VaR". Estrategia de derivados.
- ^ Aaron Brown (Marzo de 1997), Los próximos desastres diez VaREstrategia derivados
- ^ Wilmott, Paul (2007). Paul Wilmott introduce Finanzas Cuantitativas. Wiley. ISBN978-0-470-31958-1.
- ^ Lawrence York (2009), Mejores prácticas de gobernabilidad
- ^ Artzner, Philippe; Delbaen, Freddy; Eber, Jean-Marc; Heath, David (1999). "Medidas coherentes de riesgo" (pdf). Matemática financiera 9 (3): 203-228. Doi:10.1111/1467-9965.00068. 03 de febrero de 2011.
- ^ Nassim Taleb (diciembre de 1996-enero de 1997) El mundo según Nassim TalebEstrategia derivados
- ^ Julia L. Wirch; Mary R. Hardy. "Las medidas de riesgo de distorsión: coherencia y dominio estocástico" (pdf). 10 de marzo de 2012.
- ^ Balbás, A.; Garrido, J.; Mayoral, S. (2008). "Propiedades de las medidas de riesgo de distorsión". Metodología y cálculo de probabilidad aplicada 11 (3): 385. Doi:10.1007/s11009-008-9089-z.
- ^ Jorion, Philippe (abril de 1997). "El Debate Jorion-Taleb". Estrategia de derivados.
- ^ a b c d e f Aaron Brown (Junio – julio 2008). "Las ganancias privadas y riesgo socializada". Examen de riesgo GARP.
- ^ a b c Espen Haug (2007). Modelos derivados de modelos. John Wiley & Sons. ISBN978-0-470-01322-9.
- ^ Ezra Zask (febrero de 1999), Tomar la tensión de prueba de esfuerzoEstrategia derivado
- ^ a b c d e Kolman, Joe; Onak, Michael; Jorion, Philippe; Taleb, Nassim; Derman, Emanuel; Putnam, Blu; Sandor, Richard; Jonas, Stan; Dembo, Ron; Holt, George; Tanenbaum, Richard; Margrabe, William; Mudge, Dan; Lam, James; Rozsypal, Jim (abril de 1998). "Mesa redonda: los límites de los modelos". Estrategia de derivados.
- ^ Aaron Brown (Diciembre de 2007). "En tensionar el tamaño adecuado". Examen de riesgo GARP.
- ^ Markovich, N. (2007), Pruebas no paramétrico análisis de datos de cola pesada univariadoWiley
- ^ Novak, S.Y. (2011). Métodos de valor extremo con aplicaciones para financiar. Chapman & Hall/CRC Press. ISBN978-1-4398-3574-6.
- ^ McKinsey & Company. "Documentos de trabajo de McKinsey sobre riesgo, número 32" (pdf).
- ^ a b Taleb, Nassim Nicholas (2007). El cisne negro: El impacto de lo altamente Improbable. Nueva York: Random House. ISBN978-1-4000-6351-2.
- ^ Nassim Taleb (abril de 1997), El Debate Jorion-TalebEstrategia derivados
- ^ David Einhorn (junio – julio 2008), Beneficios privados y riesgo socializadaInforme de riesgo GARP
- ^ Joe Nocera (4 de enero, 2009), Mala gestión del riesgo, El New York Times Revista
- ^ https://GOP.Science.House.gov/media/Hearings/oversight09/sept10/Taleb.pdf
Enlaces externos
- Discusión
- "Valor en riesgo", Ben SopranzettiCPA pH.d.,
- "Las tormentas perfectas" – hermoso y verdadero radica en la gestión de riesgos, Satyajit Das
- "Gloria Mundi" – todo acerca de valor en riesgoSchachter Barry
- Mala gestión del riesgo, Joe Nocera NYTimes artículo.
- "VaR no tiene que ser duro"Tanenbaum Rich
- Herramientas
- Calculadora online de VaR en tiempo realPascalau Razvan, Universidad de Alabama
- Valor en riesgo (VaR)Benninga Simon y Zvi Wiener. (Mathematica en educación e investigación Vol. 7 Nº 4 1998.)
- Revista Estrategia derivados. "Dentro de D. E. Shaw" Comercio y gestión 1998 del riesgo
|
||||||||||||||||||||||||||||||||||||
Otras Páginas
- Hipotesis extraterrestre
- Tablero de instrumentos (negocio)
- Cromatografia de gases
- Guardia (seguridad de la informacion)
- Internet Plus
- Nikki Catsouras fotografias controversia (categoria California Highway Patrol)
- Charles Jacobs (juez de Louisiana) (abogados categoria de ciudad y ciudad en los Estados Unidos)
- Diccionario de datos