Relación señal a ruido cuantización
|
|
Este artículo incluye un lista de referencias, relacionados con la lectura o enlaces externos, pero sus orígenes no están claros porque carece de citas en línea. (Septiembre de 2011) |
Relación señal a ruido cuantización (SQNR o SNqR) es ampliamente utilizado a medida de la calidad en el análisis digitalización esquemas como el PCM)modulación por impulsos codificados) y codecs multimedia. El SQNR refleja la relación entre la máxima nominal intensidad de la señal y el error de cuantización (también conocido como ruido de cuantización) introducido en el conversión de analógico a digital.
La fórmula SQNR se deriva de la general (SNRRelación señal / ruído) fórmula para el pulso-código binario modulada canal de comunicación:
donde
-
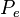 es la probabilidad de error de bit recibidos
es la probabilidad de error de bit recibidos
-
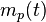 es el nivel de señal de mensaje de pico
es el nivel de señal de mensaje de pico
-
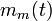 es el nivel de señal de mensaje media
es el nivel de señal de mensaje media
Como SQNR se aplica a quantized señales, las fórmulas para SQNR refieren a tiempo discreto de señales digitales. En lugar de  , utilizaremos la señal digitalizada
, utilizaremos la señal digitalizada 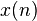 . Para
. Para  pasos de cuantización, cada muestra,
pasos de cuantización, cada muestra,  requiere
requiere 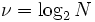 brocas. El función de distribución de probabilidad (pdf) que representa la distribución de valores en
brocas. El función de distribución de probabilidad (pdf) que representa la distribución de valores en  y puede ser denotado como
y puede ser denotado como  . El valor máximo de la magnitud de cualquier
. El valor máximo de la magnitud de cualquier  se denota por
se denota por  .
.
Como SQNR, como SNR, es una relación de potencia de señal poder algún ruido, se puede calcular como:
La potencia de la señal es:
La potencia de ruido de cuantización puede expresarse como:
Dando:
Cuando se desea la SQNR en términos de Decibelios (dB), es una aproximación útil a SQNR:
donde  es el número de bits en una muestra cuantificada, y
es el número de bits en una muestra cuantificada, y 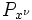 se calcula la potencia de la señal por encima. Tenga en cuenta que para cada bit agregado a una muestra, el SQNR sube por aproximadamente 6dB)
se calcula la potencia de la señal por encima. Tenga en cuenta que para cada bit agregado a una muestra, el SQNR sube por aproximadamente 6dB) ).
).
Referencias
- B.P.Li, moderna Digital y sistemas de comunicación analógicos (tercera edición), Oxford University Press, 1998
Enlaces externos
- Señal a ruido de cuantización en quantized sinusoidal -Análisis de error del quantization en una onda sinusoidal
|
||||||||||||||||||||||||||

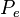 es la probabilidad de error de bit recibidos
es la probabilidad de error de bit recibidos
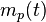 es el nivel de señal de mensaje de pico
es el nivel de señal de mensaje de pico
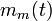 es el nivel de señal de mensaje media
es el nivel de señal de mensaje media
![\mathrm{SQNR} = \frac{P_{signal}}{P_{noise}} = \frac{E[x^2]}{E[\tilde{x}^2]}](http://upload.wikimedia.org/math/8/4/c/84c4d6e17e7ecbe4c6fa55de2206e474.png)
![\overline{x^2} = E[x^2] = P_{x^\nu}=\int_{}^{}x^2f(x)dx](http://upload.wikimedia.org/math/2/1/0/210d3d3fd4b66220fa0f4b44bc6f3d8c.png)
![E[\tilde{x}^2] = \frac{x_{max}^2}{3\times4^\nu}](http://upload.wikimedia.org/math/4/2/7/42765f5b32bfb2e99af6c26891447dd3.png)

