Programación tasa monotónica

En Ciencias de la computación, programación tasa monotónica (RMS) es un algoritmo de planificación utilizado en sistemas operativos en tiempo real con una clase de programación de prioridad estática. Las prioridades estáticas están asignadas sobre la base de la duración del ciclo del trabajo: cuanto más corta es la duración del ciclo, mayor es prioridad el trabajo es.

Estos sistemas operativos son generalmente preventivo y deterministas garantías con respecto a los tiempos de respuesta. Análisis monotónica tasa se utilizan en conjunción con los sistemas para proporcionar garantías de programación para una aplicación particular.

Introducción

Una versión sencilla de tasa monotónica análisis asume que hilos tienen las siguientes propiedades:

• No hay intercambio de recursos (procesos no comparten recursos, por ejemplo un hardware recursos, una cola o cualquier tipo de semáforo (bloqueo o sin bloqueoocupado-espera))
• Plazos deterministas son exactamente iguales a los períodos
• Prioridades estáticas (la tarea con la más alta prioridad estática que puede ejecutar inmediatamente previene todas las demás tareas)
• Estáticas prioridades asignadas según la ritmo monótono convenios (tareas con períodos/plazos más cortos se dan una mayor prioridad)
• Contexto interruptor de tiempos y otras operaciones de hilo son libres y no tienen impacto en el modelo

Es un modelo matemático que contiene una simulación calculada de períodos en un sistema cerrado, donde round robin y tiempo compartido programadores capaces de satisfacer las necesidades de programación lo contrario. Ritmo monótono programación Mira un modelado de ejecución de todos los subprocesos en el sistema y determina cuánto tiempo es necesario para cumplir con las garantías para el conjunto de hilos en cuestión.

Liu & Layland (1973) demostró que un conjunto de n tareas periódicas con períodos únicas, existe un calendario factible que siempre cumplen con los plazos si el CPU utilización está por debajo de un específico enlazada (dependiendo del número de tareas). Es la prueba de planificación para RMS:

$U = \sum_{i=1}^{n} \frac{C_i}{T_i} \leq n({2}^{1/n} - 1)$

donde C_i es el tiempo de cómputo, T_i es el periodo de lanzamiento (con plazo de un período más adelante), y n es el número de procesos que se programe. Por ejemplo, U ≤ 0.8284 para dos procesos. Cuando el número de procesos tiende a infinito, esta expresión tenderá hacia:

$\lim_{n \rightarrow \infty} n(\sqrt[n]{2} - 1) = \ln 2 \approx 0.693147\ldots$

Así que una estimación aproximada es que RMS en el caso general puede cumplir todos los plazos si la CPU es 69.3%. El 30,7% de la CPU puede ser dedicado a tareas en tiempo real no menor prioridad. Es sabido que un sistema de tareas periódicas generadas al azar reunirá todos los plazos cuando la utilización es 85% o menos, Sin embargo este hecho depende de conocer las estadísticas de tarea exacta (periodos, plazos) que no pueden ser garantizadas para todos conjuntos de tareas.

El ritmo monótono asignación de prioridad es óptima lo que significa que si cualquier prioridad estática algoritmo de planificación puede cumplir todos los plazos, entonces el ritmo monótono algoritmo puede también. El programación de fecha límite monotónica algoritmo también es óptima con períodos iguales y plazos, de hecho en este caso que los algoritmos son idénticos; Además, plazo monotónica programación es óptimo cuando los plazos son menos períodos. Para el modelo de tarea en la cual los plazos pueden ser mayores que períodos, algoritmo de Audsley dotado de una prueba exacta planificación para este modelo encuentra una asignación óptima de prioridad.

Evitando la inversión prioritaria

En muchas aplicaciones prácticas, los recursos son compartidos y los no modificados RMS estarán sujetos a inversión prioritaria y interbloqueo peligros. En la práctica, esto se resuelve mediante la desactivación de preferencia o por herencia de prioridad. Deben usar métodos alternativos cerradura algoritmos gratis o evitar el uso compartido de un mutex/semáforo en subprocesos con prioridades diferentes. Esto es para que no se pueden provocar conflictos por los recursos en primer lugar.

Desactivación de preferencia

• El OS_ENTER_CRITICAL() y OS_EXIT_CRITICAL() primitivas que traben CPU interrupciones en un núcleo en tiempo real, por ejemplo MicroC/OS-II
• El splx() familia de primitivas que anidan la fijación de las interrupciones del dispositivo (FreeBSD 5.x/6.x),

Herencia de prioridad

• El Protocolo de herencia prioridad básica promueve la prioridad de la tarea que tiene el recurso a la prioridad de la tarea que pide ese recurso en el momento de que la solicitud. Tras su liberación del recurso, se restablece el nivel de prioridad original antes de la promoción. Este método no impide los interbloqueos y sufre de encadenado de bloqueo. Es decir, si una tarea de alta prioridad tiene acceso a múltiples recursos compartidos en secuencia, tenga que esperar (bloque) en una tarea de prioridad más baja para cada uno de los recursos. El parche en tiempo real para el Kernel de Linux incluye una aplicación de este protocolo.

• El Protocolo de taquilla más alta plantea la prioridad de la tarea durante el uso de un recurso a las más altas entre las prioridades de todas las tareas que alguna vez utilizan ese recurso. El techo de prioridad para cada recurso puede ser precomputed en tiempo de diseño del sistema. Este protocolo evita los interbloqueos y límites el tiempo de bloqueo en a lo más la longitud de una sección crítica de prioridad baja.

• El Protocolo de techo prioridad realza la prioridad básica herencia protocolo asignando un prioridad de techo cada semáforo, que es la prioridad del trabajo más alta que jamás accederá a ese semáforo. Un trabajo no puede tener preferencia sobre una sección crítica de menor prioridad si su prioridad es menor que la prioridad de techo para esa sección. Este método evita los interbloqueos y límites el tiempo de bloqueo en a lo más la longitud de una sección crítica de prioridad baja. Este método puede ser subóptima, que puede causar bloqueo innecesario. El protocolo de techo de prioridad está disponible en el VxWorks núcleo en tiempo real.

Algoritmos de herencia de prioridad pueden ser caracterizados por dos parámetros. En primer lugar, es la herencia perezoso (sólo cuando es imprescindible) o inmediata (aumentar prioridad antes que haya un conflicto). En segundo lugar está la herencia optimista (impulso una cantidad mínima) o pesimista (alza en más de la cantidad mínima):

	pesimista	optimista
inmediata	OS_ENTER_CRITICAL() / OS_EXIT_CRITICAL()	splx(), la taquilla más alta
perezoso		Protocolo de prioridad techo, prioridad básica herencia protocolo

En la práctica no hay diferencias matemática (en cuanto a la utilización del sistema Liu-Layland enlazada) entre los algoritmos de perezosos e inmediatos y son más eficientes para implementar los algoritmos de inmediatos, y así son los utilizados por sistemas más prácticos.

Un ejemplo del uso de la herencia de prioridad básica está relacionado con el "Mars Pathfinder Reset de fallo" cambiando los parámetros de creación para el semáforo para permitir la herencia de prioridad que se fijó en Marte.

Ejemplo

Proceso	Tiempo de ejecución	Período
P1	1	8
P2	2	5
P3	2	10

La utilización será:

$\frac{1}{8} + \frac{2}{5} + \frac{2}{10} = 0.725$

La condición suficiente para 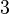$3\,$ procesos, bajo el cual podemos concluir que el sistema es programable es:

$U = 3(2^\frac{1}{3} - 1) = 0.77976\ldots$

Desde $0.725 < 0.77976\ldots$ el sistema es seguramente programable.

Pero recuerde, esta condición no es necesaria. Así que no podemos decir que un sistema con una mayor utilización no es programable con este algoritmo de planificación.

Véase también

• Deos, un tiempo y espacio reparten sistema operativo en tiempo real que contiene un Scheduler monótono ritmo de trabajo.
• Programación de fecha límite monotónica
• Prioridad dinámica programación
• Lo más temprano posible plazo primero programación
• RTEMS, una fuente abierta sistema operativo en tiempo real que contiene un Scheduler monótono ritmo de trabajo.
• Programación (informática)

Lectura adicional

• Buttazzo, Giorgio (2011), Sistemas informáticos en tiempo real duro: Algoritmos de programación predecibles y aplicacionesNueva, Nueva York: Springer.
• Alan Burns y Andy Wellings (2009), Lenguajes de programación y sistemas en tiempo real (4ª ed.), Addison-Wesley, ISBN978-0-321-41745-9
• Liu, Jane W.S. (2000), Sistemas de tiempo realUpper Saddle River, NJ: Prentice HallCapítulo 6.
• Joseph, M.; Pandya, P. (1986), "Tiempos de hallazgo de respuesta en sistemas de tiempo real", Diario de informática BCS 29 (5): 390-395, Doi:10.1093/comjnl/29.5.390.
• Sha, Lui; Goodenough, John B. (abril de 1990), "Teoría y Ada de programación de tiempo real", IEEE Computer 23 (4): 53-62, Doi:10.1109/2.55469

Enlaces externos

• Mars Pathfinder Bug de investigación @ Microsoft
• Lo que realmente sucedió en Marte Rover Pathfinder por Mike Jones desde la recopilación de los riesgos, Vol. 19, número 49

Otras Páginas

• HP OmniGo 100
• Eupithecia scabrogata
• EstDomains
• Seleccion de futbol de escuela secundaria de USA hoy todos-Estados Unidos
• Helluland
• Tatsuta polder compuertas
• Creighton Molinero