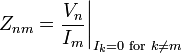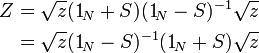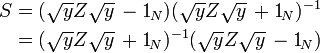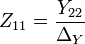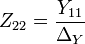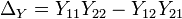Parámetros de impedancia
Parámetros de impedancia o Z-parámetros (los elementos de un matriz de impedancia o Matriz de Z) se utilizan las propiedades en Ingeniería eléctrica, Ingeniería electrónica, y sistemas de comunicación Ingeniería para describir el comportamiento eléctrico de lineal redes eléctricas. También se utilizan para describir el pequeña señal (linealizado) respuesta de redes no lineales. Son miembros de una familia de parámetros similares utilizados en ingeniería electrónica, otros ejemplos están: S-parámetros,[1] Y parámetros,[2] H-parámetros, T-parámetros o ABCD-parámetros.[3][4]
Z-parámetros también son conocidos como parámetros de impedancia de circuito abierto como se calculan bajo circuito abierto condiciones. es decir, quex= 0, donde x = 1, 2 se refieren a la entrada y salida de las corrientes que fluyen a través de los puertos (de un red de dos puertos en este caso) respectivamente.
Contenido
- 1 La matriz de parámetros Z
- 2 Redes de dos puertos
- 2.1 Relaciones de impedancia
- 3 Relación con parámetros de S
- 3.1 Dos puertos
- 4 Relación con parámetros Y
- 5 Notas
- 6 Referencias
- 7 Bibliografía
- 8 Véase también
La matriz de parámetros Z
Una matriz Z-parámetro describe el comportamiento de cualquier red eléctrica lineal que puede considerarse como un caja negra con un número de puertos. A Puerto en este contexto es un par de terminales eléctricos iguales y enfrente de las corrientes en y fuera de la red y teniendo un particular voltaje entre ellos. La matriz Z no da ninguna información sobre el comportamiento de la red cuando no están equilibradas las corrientes en cualquier puerto de esta manera (esto posible), ni le da ninguna información sobre la tensión entre los terminales no pertenecientes al mismo puerto. Por lo general, se pretende que cada conexión a la red externa está entre los terminales de un puerto, para que estas limitaciones son apropiadas.
Para una definición genérica red multipuerto, se asume que cada uno de los puertos se asigna un número entero n que van desde 1 a N, donde N es el número total de puertos. Para el puerto n, la definición de Z-parámetro asociada es en cuanto al puerto de corriente y voltaje de puerto,  y
y  respectivamente.
respectivamente.
Para todos los puertos las tensiones pueden definirse en términos de la matriz de parámetros Z y las corrientes por la siguiente ecuación de matriz:
donde Z es una N × N matriz de los elementos de los cuales pueden ser indexados usando convencional matriz notación. En general son los elementos de la matriz de parámetros Z números complejos y funciones de la frecuencia. Para una red de un puerto, la matriz Z se reduce a un solo elemento, siendo lo normal impedancia mide entre los dos terminales.Los parámetros Z son también conocidos como los parámetros del circuito abierto en cuanto a su determinación que es necesario abrir un puerto de circuito y analizar las corrientes y voltajes a través de otros puertos.
Redes de dos puertos


La matriz Z-parámetro para el red de dos puertos es probablemente el más común. En este caso la relación entre las corrientes del puerto, Puerto voltajes y el Z-parámetro matrix está dada por:
-
 .
.
donde
Para el caso general de un N-red de puerto,
Relaciones de impedancia
La impedancia de entrada de una red de dos puertos viene dada por:
donde ZL es la impedancia de la carga conectada al puerto dos.
Del mismo modo, la impedancia de salida viene dada por:
donde ZS es la impedancia de la fuente conectada al puerto uno.
Relación con parámetros de S
Los parámetros de una red de Z se relacionan con su S-parámetros por[5]
-
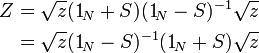
y[5]
-
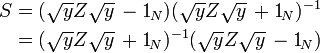
donde  es el matriz identidad,
es el matriz identidad,  es un matriz diagonal teniendo la raíz cuadrada de la Impedancia característica en cada puerto como elementos distintos de cero,
es un matriz diagonal teniendo la raíz cuadrada de la Impedancia característica en cada puerto como elementos distintos de cero,

y  es la matriz diagonal correspondiente de raíces cuadradas de admitancias característicos. En estas expresiones las matrices representadas por los factores entre corchetes conmutar y entonces, como se muestra arriba, puede escribirse en cualquier orden.[5][Nota 1]
es la matriz diagonal correspondiente de raíces cuadradas de admitancias característicos. En estas expresiones las matrices representadas por los factores entre corchetes conmutar y entonces, como se muestra arriba, puede escribirse en cualquier orden.[5][Nota 1]
Dos puertos
En el caso especial de una red de dos puertos, con la misma impedancia característica  en cada puerto, reducen las expresiones anteriores a
en cada puerto, reducen las expresiones anteriores a
Donde
Los dos puertos S-parámetros pueden obtenerse los equivalentes cuadripolo Z-parámetros por medio de las siguientes expresiones[6]
donde
Las expresiones anteriores generalmente utilizará números complejos para  y
y  . Tenga en cuenta que el valor de
. Tenga en cuenta que el valor de 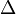 puede convertirse en 0 para valores específicos del
puede convertirse en 0 para valores específicos del  la división por
la división por 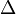 en los cálculos de
en los cálculos de  puede llevar a una división por 0.
puede llevar a una división por 0.
Relación con parámetros Y
Conversión de Y parámetros a Z-parámetros es mucho más simple, como la matriz de parámetros Z es sólo el inversa de la matriz Y parámetros. Para un dos puertos:
donde
es el determinante de la matriz Y parámetros.
Notas
- ^ Cualquier matriz cuadrada conmuta con sí mismo y con la matriz identidad y si dos matrices A y B viaje, así que a continuación A y B-1 (desde AB-1=B-1BAB-1=B-1ABB-1=B-1A)
Referencias
- ^ David M. Pozar (2004-02-05). Ingeniería de microondas. Wiley. págs. 170-174. ISBN978-0-471-44878-5.
- ^ David M. Pozar, 2005 (op. cit.); PP 170-174.
- ^ David M. Pozar, 2005 (op. cit.); PP 183-186.
- ^ A.H. Morton, Avanzada ingeniería eléctricaPitman Publishing Ltd., 1985; pp 33-72, ISBN 0-273-40172-6.
- ^ a b c Russer, Peter (2003). Electromagnetismo, diseño de circuito y antena para ingeniería de comunicaciones de microondas. Artech House. ISBN1-58053-532-1.
- ^ Simon Ramo; John R. Whinnery; Theodore Van Duzer (1994-02-09). Campos y ondas en la comunicación electrónica. Wiley. págs. 537 – 541. ISBN978-0-471-58551-0.
Bibliografía
- David M. Pozar (2004-02-05). Ingeniería de microondas. Wiley. ISBN978-0-471-44878-5.
- Simon Ramo; John R. Whinnery; Theodore Van Duzer (1994-02-09). Campos y ondas en la comunicación electrónica. Wiley. ISBN978-0-471-58551-0.
Véase también
- Parámetros de dispersión
- Parámetros de admisión
- Red de dos puertos

 .
.