Medida del riesgo
En matemáticas financieras, un medida del riesgo se utiliza para determinar la cantidad de un activo o conjunto de activos (tradicionalmente moneda) para mantenerse en reserva. El objetivo de esta reserva es hacer el riesgos tomada por instituciones financieras, como bancos y compañías de seguros, aceptables para el regulador. En los últimos años se ha convertido atención hacia medida de riesgo coherente y convexo.
Contenido
- 1 Matemáticamente
- 2 Conjunto de valores
- 2.1 Matemáticamente
- 3 Ejemplos
- 3.1 Medidas de riesgo bien conocido
- 3.2 Varianza
- 4 Relación al conjunto de aceptación
- 4.1 Medida del riesgo al conjunto de aceptación
- 4.2 Aceptación a medida del riesgo
- 5 Relación con la medida del riesgo de desviación
- 6 Véase también
- 7 Referencias
- 8 Lectura adicional
Matemáticamente
Una medida del riesgo se define como una asignación de un conjunto de variables aleatorias a los números verdaderos. Este conjunto de variables aleatorias representa devoluciones de cartera. La notación común para una medida del riesgo asociada a una variable aleatoria  es
es  . Una medida del riesgo
. Una medida del riesgo  debe tener ciertas propiedades:[1]
debe tener ciertas propiedades:[1]
- Normalizado
-

- Traslativo
-

- Monotono
-

Conjunto de valores
En una situación con  -valorado carteras que riesgo puede medirse en
-valorado carteras que riesgo puede medirse en  de los activos, entonces un conjunto de carpetas es la forma correcta de representar riesgo. Medidas de riesgo conjunto de valores son útiles para los mercados con costos de transacción.[2]
de los activos, entonces un conjunto de carpetas es la forma correcta de representar riesgo. Medidas de riesgo conjunto de valores son útiles para los mercados con costos de transacción.[2]
Matemáticamente
Una medida del riesgo valores de conjunto es una función  , donde
, donde  es un
es un  -dimensional Espacio LP,
-dimensional Espacio LP,  , y
, y 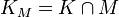 donde
donde  es una constante cono de solvencia y
es una constante cono de solvencia y  es el conjunto de carpetas de la
es el conjunto de carpetas de la  bienes de referencia.
bienes de referencia.  debe tener las siguientes propiedades:[3]
debe tener las siguientes propiedades:[3]
- Normalizado
-
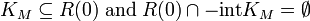
- Traslativo de M
-

- Monotono
-

Ejemplos
Medidas de riesgo bien conocido
- Valor en riesgo
- Déficit esperado
- Expectativa condicional cola
- Medida del riesgo entrópica
- Precio Superhedging
- ...
Varianza
Varianza (o desviación estándar) es No una medida del riesgo. Esto se puede ver ya que tiene la propiedad de traducción ni moniticidad. Es decir  para todos
para todos  , y se puede encontrar un contraejemplo simple para moniticidad. La desviación estándar es un medida del riesgo de desviación.
, y se puede encontrar un contraejemplo simple para moniticidad. La desviación estándar es un medida del riesgo de desviación.
Relación al conjunto de aceptación
Hay un uno-a-uno correspondencia entre un conjunto de aceptación y una medida de riesgo correspondiente. Como definido abajo puede ser demostrado que 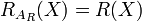 y
y  .[4]
.[4]
Medida del riesgo al conjunto de aceptación
- If
 Entonces es una medida del riesgo (escalar)
Entonces es una medida del riesgo (escalar)  es un conjunto de aceptación.
es un conjunto de aceptación. - If
 Entonces es una medida de riesgo conjunto valorado
Entonces es una medida de riesgo conjunto valorado  es un conjunto de aceptación.
es un conjunto de aceptación.
Aceptación a medida del riesgo
- If
 es una aceptación establecida entonces (en 1-d)
es una aceptación establecida entonces (en 1-d) 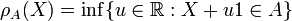 define una medida del riesgo (escalar).
define una medida del riesgo (escalar). - If
 es una aceptación entonces
es una aceptación entonces  es una medida de riesgo conjunto de valores.
es una medida de riesgo conjunto de valores.
Relación con la medida del riesgo de desviación
Hay un uno-a-uno relación entre un medida del riesgo de desviación D y una medida limitada expectativa de riesgo  donde para cualquier
donde para cualquier 
![D(X) = \rho(X - \mathbb{E}[X])](//upload.wikimedia.org/math/c/9/0/c90db87af3aa86a9480fc0281ccef7fa.png)
![\rho(X) = D(X) - \mathbb{E}[X]](//upload.wikimedia.org/math/7/c/b/7cb0cc8818e1bfe2cf26aed6bfd743b5.png) .
.
 se llama esperanza limitada si satisface
se llama esperanza limitada si satisface ![\rho(X) > \mathbb{E}[-X]](http://upload.wikimedia.org/math/a/7/7/a7795d7e4730e72fa0f4d899d07ed88f.png) para cualquier nonconstant X y
para cualquier nonconstant X y ![\rho(X) = \mathbb{E}[-X]](http://upload.wikimedia.org/math/3/3/3/333bbe7f31e3642b13af07ea5e73af5e.png) para cualquier constante X.[5]
para cualquier constante X.[5]
Véase también
- Medida de riesgo coherente
- Medida del riesgo dinámico
- Contabilidad de gestión de riesgo
- Gestión del riesgo
- Métricas de riesgo -el concepto abstracto que cuantifica una medida del riesgo
- RiskMetrics -un modelo de gestión de riesgos
- Medida del riesgo espectral
- Medida del riesgo de distorsión
- Valor en riesgo
- Valor en riesgo condicional
- Entrópico valor en riesgo
- Riesgo relativo retorno
Referencias
- ^ Artzner, Philippe; Delbaen, Freddy; Eber, Jean-Marc; Heath, David (1999). "Medidas coherentes de riesgo" (pdf). Matemática financiera 9 (3): 203-228. Doi:10.1111/1467-9965.00068. 03 de febrero de 2011.
- ^ Jouini, Elyes; Meddeb, Moncef; Touzi, Nizar (2004). "Medidas de riesgo coherentes vector – valorado". Finanzas y Stochastics 8 (4): 531-552. Doi:10.1007/s00780-004-0127-6.
- ^ Hamel, A. H.; Heyde, f el. (2010). "Dualidad por valor conjunto de medidas de riesgo" (pdf). SIAM Journal on matemáticas financieras 1 (1): 66 – 95. Doi:10.1137/080743494. 17 de agosto de 2012.
- ^ Andreas H. Hamel; Frank Heyde; Birgit Rudloff (2011). "Medidas de riesgo conjunto de valores para los modelos de mercado cónico" (pdf). Matemáticas y economía financiera 5 (1): 1 – 28. Doi:10.1007/s11579-011-0047-0. 20 de abril de 2012.
- ^ Rockafellar, Tyrrell; Uryasev, Stanislav; Zabarankin, Michael (2002). "Medidas de desviación en optimización y análisis de riesgos" (pdf). 13 de octubre de 2011.
Lectura adicional
- Crouhy, Michel; D. Galai; R. Mark (2001). Gestión del riesgo. McGraw-Hill. págs. 752 páginas. ISBN 0-07-135731-9.
- Kevin, Dowd (2005). Medición de riesgo de mercado (2ª ed.). John Wiley & Sons. págs. 410 páginas. ISBN 0-470-01303-6.
- Foellmer, Hans; Schied, Alexander (2004). Finanzas estocástico. de Gruyter serie en matemáticas 27. Berlín: Walter de Gruyter. págs. xi + 459. ISBN311-0183463. MR2169807.
- Shapiro, Alexander; Dentcheva, Darinka; Ruszczyński, Andrzej (2009). Conferencias sobre programación estocástica. Modelado y teoría. Serie MPS/SIAM en optimización 9. Philadelphia: Sociedad para la matemática Industrial y aplicada. PP. xvi + 436. ISBN978-0898716870. MR2562798.



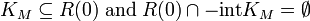


 es un conjunto de aceptación.
es un conjunto de aceptación. es un conjunto de aceptación.
es un conjunto de aceptación. es una aceptación establecida entonces (en 1-d)
es una aceptación establecida entonces (en 1-d) 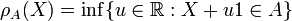 define una medida del riesgo (escalar).
define una medida del riesgo (escalar). es una medida de riesgo conjunto de valores.
es una medida de riesgo conjunto de valores.![D(X) = \rho(X - \mathbb{E}[X])](http://upload.wikimedia.org/math/c/9/0/c90db87af3aa86a9480fc0281ccef7fa.png)
![\rho(X) = D(X) - \mathbb{E}[X]](http://upload.wikimedia.org/math/7/c/b/7cb0cc8818e1bfe2cf26aed6bfd743b5.png) .
.