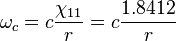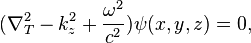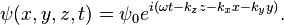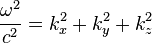Frecuencia de corte
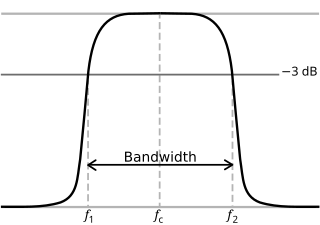

En física y Ingeniería eléctrica, un frecuencia de corte, frecuencia de la esquina, o frecuencia de descanso es un límite en un sistema respuesta de frecuencia en el que la energía que fluye a través del sistema comienza a ser reducido)atenuada o reflejado) en lugar de paso.
Normalmente, en sistemas electrónicos tales como filtros y canales de comunicación, frecuencia de corte se aplica a una arista en una MJ, pasa-altos, bandpass, o Suprime banda característica – una frecuencia caracterizar un límite entre un ancho de banda y del stopband. A veces se toma como el punto en la respuesta del filtro donde un banda de transición y ancho de banda, por ejemplo, tal como se define por 3dB esquina (una frecuencia para que la salida del circuito es −3 dB del valor nominal de ancho de banda). Por otra parte, un stopband frecuencia puede especificarse como un punto donde una banda de transición y un stopband cumplir: una frecuencia para la cual la atenuación es más grande que la atenuación del stopband requerida, que por ejemplo puede ser 30 dB o 100 dB.
En el caso de un Guía de onda o un antena, las frecuencias de corte corresponden a la inferior y superior longitudes de onda de corte.
Contenido
- 1 Electrónica
- 1.1 Ejemplo de la función de transferencia del solo-poste
- 1.2 Filtros Chebyshev
- 2 Comunicaciones
- 3 Guías de onda
- 3.1 Análisis matemático
- 4 Véase también
- 5 Referencias
- 6 Enlaces externos
Electrónica
En electrónica, frecuencia de corte o frecuencia es el frecuencia por encima o por debajo que la potencia de salida de un circuito, tales como un línea, amplificador, o filtro electrónico se ha reducido a una proporción dada de la energía en el ancho de banda. Con mayor frecuencia esta proporción es mitad el poder de banda pasante, también conocido como el 3dB punto desde una caída de 3 dB corresponde aproximadamente a la mitad de potencia. Como una relación de tensión es una caída a  de la tensión de la banda pasante.[1] Otras relaciones además de los 3 puntos de dB puede también ser relevante, por ejemplo ver filtros Chebyshev abajo.
de la tensión de la banda pasante.[1] Otras relaciones además de los 3 puntos de dB puede también ser relevante, por ejemplo ver filtros Chebyshev abajo.
Ejemplo de la función de transferencia del solo-poste
El filtro de paso bajo simple función de transferencia,
-
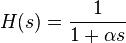 ,
,
tiene un único Polo en s = -1/Α. La magnitud de esta función en la jω avión
-
 .
.
En el corte
-
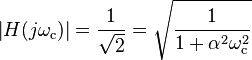 .
.
Por lo tanto, la frecuencia de corte está dada por
-
 .
.
Donde s es el s-avión variable, ω es frecuencia angular y j es el unidad imaginaria.
Filtros Chebyshev
A veces otros cocientes son más convenientes que el punto 3 del dB. Por ejemplo, en el caso de la Filtro de Chebyshev es usual para definir la frecuencia de corte como el punto después del último pico en la respuesta de frecuencia en la que el nivel ha caído en el valor de diseño de la ondulación de ancho de banda. La cantidad de rizo en esta clase de filtro puede ser fijada por el diseñador a cualquier valor deseado, por lo tanto, la proporción utilizada puede ser cualquier valor.[2]
Comunicaciones
En comunicaciones, la frecuencia de corte del término puede significar la frecuencia por debajo del cual una ondas de radio es incapaz de penetrar en una capa de la ionosfera en el ángulo de incidencia necesario para transmisión entre dos puntos especificados por reflexión de la capa.
Guías de onda
La frecuencia de corte de un Guía de ondas electromagnética es la frecuencia más baja para la cual un modo se propagará en él. En fibra óptica, es más común que se considere la longitud de onda de corte, la máxima longitud de onda que se propagan en un fibra óptica o Guía de onda. La frecuencia de corte se encuentra con el ecuación característica de la Ecuación de Helmholtz para las ondas electromagnéticas, que se deriva de la ecuación de onda electromagnética estableciendo la longitudinal número de onda igual a cero y resolviendo para la frecuencia. Por lo tanto, cualquier frecuencia emocionante inferior a la frecuencia de corte a atenuar, en lugar de propagar. La derivación siguiente asume las paredes sin pérdidas. El valor de c, el velocidad de la luz, se deben tomar para ser el velocidad del grupo llena la guía de onda de luz en cualquier material.
Para una guía de onda rectangular, es la frecuencia de corte
donde los enteros  son los números de modo, y a y b las longitudes de los lados del rectángulo. Para los modos de TE,
son los números de modo, y a y b las longitudes de los lados del rectángulo. Para los modos de TE,  (pero
(pero  No está permitido), mientras que para los modos TM
No está permitido), mientras que para los modos TM  .
.
La frecuencia de corte del TM01 modo (próxima superior de modo dominante TE11) en una guía de onda de sección circular (el modo transversal magnético sin dependencia angular y menor dependencia radial) está dada por
donde  es el radio de la guía de onda, y
es el radio de la guía de onda, y 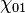 es la primera raíz de
es la primera raíz de 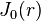 , la función Bessel de la primera clase de orden 1.
, la función Bessel de la primera clase de orden 1.
El modo dominante TE11 frecuencia de corte está dada por
-
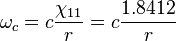 [3]
[3]
Para un fibra óptica monomodo, la longitud de onda de corte es la longitud de onda en la cual el frecuencia normalizada es aproximadamente igual a 2.405.
Análisis matemático
El punto de partida es la ecuación de onda (que se deriva de la Ecuaciones del Maxwell),
que se convierte en un Ecuación de Helmholtz teniendo en cuenta sólo las funciones de la forma
Sustitución y evaluando el derivado del tiempo da
La función  aquí se refiere a cualquier campo (el campo eléctrico o campo magnético) no tiene ningún componente del vector en la dirección longitudinal - el campo "transversal". Es una propiedad de todos los eigenmodes de la guía de onda electromagnética que al menos uno de los dos campos es transversal. El z eje se define como el eje de la guía de onda.
aquí se refiere a cualquier campo (el campo eléctrico o campo magnético) no tiene ningún componente del vector en la dirección longitudinal - el campo "transversal". Es una propiedad de todos los eigenmodes de la guía de onda electromagnética que al menos uno de los dos campos es transversal. El z eje se define como el eje de la guía de onda.
El derivado "longitudinal" en el Laplaciano puede reducirse aún más teniendo en cuenta sólo las funciones de la forma
donde  es el longitudinal Wavenumber, dando por resultado
es el longitudinal Wavenumber, dando por resultado
donde el subíndice T indica un laplaciano transversal bidimensional. El paso final depende de la geometría de la guía de onda. La geometría más fácil a resolver es la guía de onda rectangular. En ese caso puede evaluarse el resto de los laplaciano a su ecuación característica teniendo en cuenta las soluciones de la forma
Por lo tanto para la guía rectangular se evalúa el laplaciano y llegamos a
Puede especificar el wavenumbers transversal de las condiciones de límite de onda para un autobloqueantes de geometría rectangular con unas dimensiones a y b:
donde n y m los dos enteros representan un eigenmode específico. Realizar la sustitución definitiva, obtenemos
cual es el relación de dispersión en la guía de onda rectangular. La frecuencia de corte 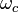 es la frecuencia crítica entre la propagación y atenuación, que corresponde a la frecuencia en la cual el wavenumber longitudinal
es la frecuencia crítica entre la propagación y atenuación, que corresponde a la frecuencia en la cual el wavenumber longitudinal  es cero. Es dada por
es cero. Es dada por
Las ecuaciones de onda también son válidas por debajo de la frecuencia de corte, donde el número de onda longitudinal es imaginario. En este caso, el campo decae exponencialmente a lo largo del eje de guía de onda y la onda es así evanescente.
Véase también
- Frecuencia angular
- Frecuencia de corte espacial (en sistemas ópticos)
- Ancho máximo media
- Filtro de paso alto
- Filtro de paso bajo
- Constante de tiempo
- Efecto Miller
Referencias
- ^ Van Valkenburg, M. E. Análisis de redes (3ª edición ed.). PP. 383, 384. ISBN0-13-611095-9. de 2008-06-22.
- ^ Mathaei, joven, Jones Filtros de microondas, redes de impedancia y estructuras de acoplamiento, poniendo-86, 1964 McGraw-Hill.
- ^ I. C. Hunter, Teoría y diseño de filtros de microondas, p.214 IET, 2001 ISBN 0-85296-777-2.
 Este artículo incorporamaterial de dominio público desde el Administración de servicios generales documento "Federal estándar 1037C" (en apoyo de MIL-STD-188).
Este artículo incorporamaterial de dominio público desde el Administración de servicios generales documento "Federal estándar 1037C" (en apoyo de MIL-STD-188).
Enlaces externos
- Cálculo de la frecuencia central con comparación a la solución de la media aritmética y media geométrica
- Conversión de frecuencia de corte fc y el tiempo constante τ
- Información sobre las funciones de Bessel y definición matemática de
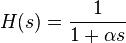 ,
,
 .
.
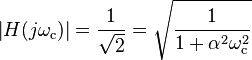 .
.
 .
.