Factor de forma (electrónica)
|
|
Este artículo Necesita referencias adicionales para verificación. (Febrero de 2013) |
En electrónica, la factor de forma de un corriente alterna forma de onda (señal) es el cociente de la RMS (Root Mean Square) valor a la valor medio (media matemática de valores absolutos de todos los puntos de la forma de onda).[1] Identifica la relación de la corriente directa de igual potencia en relación con la corriente alterna dada. El primero puede también definirse como la corriente directa que producirá calor equivalente.[2]
Contenido
- 1 Calcular el factor de forma
- 2 Aplicación
- 3 Propiedades
- 4 Factores de forma específica
- 5 Véase también
- 6 Enlaces externos
- 7 Referencias
Calcular el factor de forma
Para una función ideal, onda continua en el tiempo T, se puede calcular el RMS en integral forma:[3]
![X_\mathrm{rms} = \sqrt {{1 \over {T}} {\int_{t_0}^{t_0+T} {[f(t)]}^2\, dt}}](http://upload.wikimedia.org/math/d/d/b/ddbbfdbf89b68892dfadd1a092ce90ff.png)
El promedio rectificado es entonces la media de la integral del valor absoluto de la función:[3]
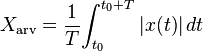
El cociente de estos dos valores es el factor de forma, 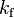 , o en situaciones de ambigüedad,
, o en situaciones de ambigüedad,  .
.
![k_\mathrm{f} = \frac \mathrm{RMS} \mathrm{ARV} = \frac{\sqrt {{1 \over {T}} {\int_{t_0}^{t_0+T} {[f(t)]}^2\, dt}}}{{1 \over {T}} {\int_{t_0}^{t_0+T} {|x(t)|\, dt}}} = \frac{\sqrt{T\int_{t_0}^{t_0+T}{{[f(t)]}^2\, dt}}}{\int_{t_0}^{t_0+T} {|x(t)|\, dt}}](http://upload.wikimedia.org/math/5/d/6/5d6682be3aad03817d49f0847ca222aa.png)
 refleja la variación en la distancia de la función de la media y es desproporcionadamente afectados por grandes desviaciones del valor promedio rectificado.[4] Siempre será al menos tan grande como
refleja la variación en la distancia de la función de la media y es desproporcionadamente afectados por grandes desviaciones del valor promedio rectificado.[4] Siempre será al menos tan grande como 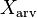 , que sólo mide la distancia absoluta de dicho promedio. Por lo tanto no puede ser menor que 1 el factor de forma (una onda cuadrada donde todos los valores momentáneos son igualmente muy por encima o por debajo del valor promedio; ver abajo), y no tiene ningún límite teórico superior para las funciones con suficiente desviación.
, que sólo mide la distancia absoluta de dicho promedio. Por lo tanto no puede ser menor que 1 el factor de forma (una onda cuadrada donde todos los valores momentáneos son igualmente muy por encima o por debajo del valor promedio; ver abajo), y no tiene ningún límite teórico superior para las funciones con suficiente desviación.

puede ser utilizado para combinar señales de diferentes frecuencias[5] (por ejemplo, para armónicos[2]), mientras que para la misma frecuencia, 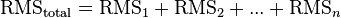 .
.
Como en el mismo dominio de ARV se puede sumar como 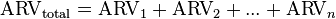 , el factor de forma de una onda compleja compuesta de varias ondas de la misma frecuencia a veces puede ser calculado como
, el factor de forma de una onda compleja compuesta de varias ondas de la misma frecuencia a veces puede ser calculado como
 .
.
Aplicación
Instrumentos de medición digitales AC se construyen a menudo con formas de onda específicas en mente. Por ejemplo, muchos multímetros digitales de la AC se escalan específicamente para mostrar el valor RMS de una onda senoidal. Puesto que el cálculo de RMS puede ser difícil de lograr digitalmente, se calcula el promedio absoluto en su lugar y el resultado multiplicado por el factor de forma de una sinusoide. Este método dará una lectura menos precisa para formas de onda que no sea una onda sinusoidal.[6]
Propiedades
Como se señaló anteriormente, el factor de forma es el cociente entre el RMS y la ARV. Las propiedades independientes y similitudes de estos dos valores definen las propiedades del factor de forma.
Por ejemplo, RMS tanto ARV son directamente proporcionales a la Amplitud  . Sin embargo, su división elimina la amplitud de la ecuación, lo que significa ese factor de forma de una determinada forma de onda es la misma sin importar cuán grande o pequeño la corriente alterna o voltaje puede ser.
. Sin embargo, su división elimina la amplitud de la ecuación, lo que significa ese factor de forma de una determinada forma de onda es la misma sin importar cuán grande o pequeño la corriente alterna o voltaje puede ser.
La cuadratura en RMS y el valor absoluto en ARV significa que tanto los valores y el factor de forma independientes de signo de la función de onda (y por lo tanto, dirección de la señal eléctrica) en cualquier momento. Por esta razón, el factor de forma es la misma para una ola de cambio de dirección con un promedio regular de 0 y su versión totalmente rectificado.
El factor de forma, 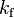 , es el más pequeño de los factores de three Waves, los otros dos están factor de cresta
, es el más pequeño de los factores de three Waves, los otros dos están factor de cresta 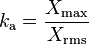 y el factor promedio menos conocidos
y el factor promedio menos conocidos  .
.
 [2]
[2]
Debido a sus definiciones (todo confía en la Root Mean Square, Valor promedio rectificado y máximo amplitud de la forma de onda), los tres factores están relacionados por 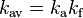 ,[2] Así se puede calcular el factor de forma con
,[2] Así se puede calcular el factor de forma con 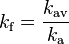 .
.
Factores de forma específica
 representa la amplitud de la función y cualquier otros coeficientes aplicados en la dimensión vertical. Por ejemplo,
representa la amplitud de la función y cualquier otros coeficientes aplicados en la dimensión vertical. Por ejemplo,  puede ser analizada como
puede ser analizada como 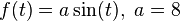 . Mientras tanto RMS y ARV son directamente proporcionales a él, no tiene ningún efecto sobre el factor de forma y puede reemplazarse con un 1 normalizado para el cálculo de ese valor.
. Mientras tanto RMS y ARV son directamente proporcionales a él, no tiene ningún efecto sobre el factor de forma y puede reemplazarse con un 1 normalizado para el cálculo de ese valor.
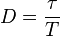 es el ciclo de deber, la relación entre el tiempo de "pulso"
es el ciclo de deber, la relación entre el tiempo de "pulso"  (cuando valor de la función no es cero) de la onda completa período
(cuando valor de la función no es cero) de la onda completa período  . Funciones más básicas de onda sólo lograr 0 por instantes infinitamente cortas y por lo tanto puede ser consideradas como teniendo
. Funciones más básicas de onda sólo lograr 0 por instantes infinitamente cortas y por lo tanto puede ser consideradas como teniendo 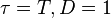 . Sin embargo, ninguna de las funciones sin pulso abajo puede ser añadida con
. Sin embargo, ninguna de las funciones sin pulso abajo puede ser añadida con 
para permitir la pulsación. Esto se ilustra con la onda senoidal rectificada de media, que puede ser considerada una sinusoide rectificada completa pulsada con 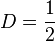 y tiene
y tiene 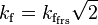 .
.
| Forma de onda | Imagen | RMS | ARV | Factor de forma |
|---|---|---|---|---|
| Onda de seno |  |
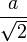 [2] [2] |
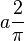 [2] [2] |
 [3] [3] |
| Senoidal rectificada de media onda |  |
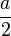 |
 |
 |
| Sinusoidal rectificada de onda completa |  |
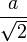 |
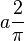 |
 |
| Onda cuadrada, valor constante |  |
 |
 |
 |
| Onda de pulso | 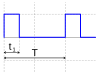 |
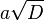 [7] [7] |
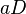 |
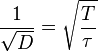 |
| Onda triangular | 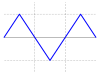 |
 [8] [8] |
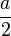 |
 |
| Onda del Sawtooth |  |
 |
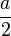 |
 |
| Ruido blanco gaussiano U(-1,1) | 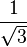 [citación necesitada] [citación necesitada] |
 [citación necesitada] [citación necesitada] |
 |
Véase también
- Factor de cresta
Enlaces externos
- Calculadora de RMS
Referencias
- ^ Stutz, Michael. "Medición de una magnitud AC". TEORÍA BÁSICA AC. 30 de mayo de 2012.
- ^ a b c d e f Dusza, Jacek; Grażyna Gortat; Antoni Leśniewski (2002). Podstawy Miernictwa (fundamentos de la medida) (en Polaco). Warszawa: Wydawnictwo Politechniki Warszawskiej. págs. 136-142, 197-203. ISBN83-7207-344-9.
- ^ a b c Jędrzejewski, Kazimierz (2007). Laboratorium Podstaw SRL (en Polaco). Varsovia: Wydawnictwo Politechniki Warszawskiej. págs. 86-87. ISBN978-83-7207-4.
- ^ "Decir Error absoluto (MAE) y significa raíz cuadrada Error (RMSE)". La organización Virtual Europea para formación meteorológica. 30 de mayo de 2012.
- ^ "Valor rms de dos ondas sinusoidales". Answers.com. 10 de junio de 2012.
- ^ Tanuwijaya, Franky. "True RMS vs AC promedio rectificado multímetro lecturas cuando se utiliza un Control de velocidad de corte de fase". ESCO Micro Pte Ltd. 13 / 12 / 2012 obtenido.
- ^ Nastase, Adrian. "Cómo obtener el valor RMS de pulso y onda cuadrada". 09 de junio de 2012.
- ^ Nastase, Adrian. "Cómo obtener el valor RMS de una onda del triángulo". 09 de junio de 2012.
Otras Páginas
- Andy Thorn (futbolista)
- Columba Bush (categoria primera damas y caballeros de la Florida)
- Interestatal 76 Nitro Pack
- Tucunduva
- Desarrollo de prueba para la deteccion de Denver
- Controversia de correo electronico de Hillary Clinton
- David Taylor (futbolista, nacido en 1883)
- Datos legibles por maquina
- Lepidoblepharis