Estructura de Weaire-Phelan
| Estructura de Weaire-Phelan | |
|---|---|
 |
|
| Grupo del espacio Notación de Fibrifold Coxeter notación |
Pm3n (223) 2o [[4,3,4]+] |
En geometría, la Estructura de Weaire-Phelan es una compleja estructura 3-dimensional que representa a un idealizado espuma de de burbujas de igual tamaño. En 1993, Trinity College Dublín físico Denis Weaire y su alumno Robert Phelan encontró que en las simulaciones de computadora de espuma, esta estructura era una mejor solución del "problema de Kelvin" que la solución anterior más conocida, la estructura de Kelvin.[1]
Contenido
- 1 La conjetura de Kelvin
- 2 Descripción de la estructura de Weaire-Phelan
- 3 Aproximación poliédrica
- 4 Aplicaciones
- 5 Ver también
- 6 Referencias
- 7 Enlaces externos
La conjetura de Kelvin

En 1887, Lord Kelvin preguntó cómo espacio podría ser dividido en celdas de igual volumen con el menor área de superficie entre ellos, es decir, ¿cuál fue la espuma de la burbuja más eficiente?[2] Este problema ya ha sido referido como el Problema de Kelvin.
Propuso una espuma, basada en la bitruncated cúbico en forma de panal, que se llama el Estructura de Kelvin. Este es el panal uniforme convexo formado por la octaedro truncado, que es un relleno de espacio frente a la 14 poliedro (un tetradecahedron), con 6 caras cuadradas y 8 caras hexagonales. De conformidad con Leyes de Plateau que rigen las estructuras de espuma, las caras hexagonales de variante de Kelvin son ligeramente curvas.
La Conjetura de Kelvin es que esta estructura resuelve el problema de Kelvin: que la espuma del panal cúbico bitruncated es la espuma más eficiente. La conjetura de Kelvin se creía ampliamente, y ningún contraejemplo era conocido por más de 100 años, hasta que fue refutada por el descubrimiento de la estructura de Weaire-Phelan.
Descripción de la estructura de Weaire-Phelan

La estructura de Weaire-Phelan difiere de Kelvin utiliza dos clases de células, aunque tienen igual volumen.
Uno es el piritoedro, irregular dodecaedro con caras pentagonales, que poseen simetría tetraédrica (Th).
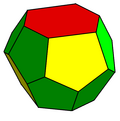
La segunda es la trapezoedro hexagonal truncado, una especie de tetrakaidecahedron con dos hexagonales y doce caras pentagonales, que poseen simetría antiprismatic (D2d).
Como los hexágonos en la estructura de Kelvin, los pentágonos en ambos tipos de células se curvan ligeramente. La superficie de la estructura de Weaire-Phelan es 0,3% menor que la de la estructura de Kelvin. No se ha demostrado que la estructura de Weaire-Phelan es óptima. Los experimentos también han demostrado que, con favorable condiciones de contorno, igual volumen de burbujas espontáneamente uno mismo-montar en el Fase de A15, cuyos átomos coinciden con los centroides de los poliedros en la estructura de Weaire-Phelan.[3]4]

Aproximación poliédrica
El poliédrico Nido de abeja asociados con el Weaire-Phelan estructura (obtenido por aplanar las caras y alisar los bordes) es también denominado libremente la estructura de Weaire-Phelan. Era conocida mucho antes de que la estructura de Weaire-Phelan fue descubierta, pero la aplicación para el problema de Kelvin fue pasado por alto.[5]
Se encuentra en dos geometrías relacionadas de estructura cristalina en química.
Donde los componentes del cristal se encuentran en los centros de los poliedros es una de las Frank – Kasper fases.6]
Donde los componentes del cristal se encuentran en las esquinas de los poliedros, es conocido como el "tipo I clathrate estructura". Hidratos de gas formado por metano, propano y dióxido de carbono a bajas temperaturas tienen una estructura en la que agua las moléculas se encuentran en los nodos de la estructura de Weaire-Phelan y son hidrógeno enlazado juntos, y las moléculas de gas más grandes se encuentran atrapadas en las jaulas poliédricas. Algunos metal alcalino siliciuros y germanides también forman esta estructura (Si/Ge en nodos, los metales del álcali en jaulas), como la sílice mineral melanophlogite (silicio en nodos, Unidos por oxígeno a lo largo de los bordes). Melanophlogite es una forma metaestable de SiO2 se estabiliza en esta estructura debido a las moléculas del gas atrapadas en las jaulas. La Internacional Zeolita La Asociación utiliza el símbolo MEP para indicar la topología marco del melanophlogite.
Aplicaciones
La estructura de Weaire-Phelan es la inspiración para el diseño de la Centro acuático nacional de Beijing para los Juegos Olímpicos de 2008 en Beijing en China.[7] El sistema estructural resultante de la ayuda es inherentemente fuerte y ligero. Como todas las uniones en la estructura están cerca tetraédrico ángulos, el marco llena un gran volumen de espacio con una cantidad reducida de material, similar a un panal de abejas hexagonal en dos dimensiones.
Ver también
- Conjetura de nido de abeja, una versión 2d de la conjetura de Kelvin.
- Superficie mínima
- Burbuja de jabón
- Conjetura de Kepler
Referencias
- ^ Weaire, D.; Phelan, R. (1994), "Un contraejemplo a la conjetura de Kelvin en superficies mínimas", Fil. MAG. Lett., 69: 107-110, doi:10.1080/09500839408241577.
- ^ Lord Kelvin (Sir William Thomson) (1887), "en la división del espacio con área mínima de particiones" (PDF), Revista filosófica, 24 (151): 503, doi:10.1080/14786448708628135.
- ^ Gabbrielli, R.; Meagher, A.J.; Weaire, D.; Brakke, K.A.; Hutzler, S. (2012), "Una realización experimental de la estructura de Weaire-Phelan en espuma líquida monodispersa", Fil. MAG. Lett., 92: 1 – 6, doi:10.1080/09500839.2011.645898.
- ^ Bola, Philip (2011), "los científicos hacen la espuma 'perfecta': teórica espuma baja energía de verdad", Naturaleza, doi:10.1038/Nature.2011.9504.
- ^ Un diagrama puede encontrarse en Pauling, Linus (1960). La naturaleza del enlace químico (3ª Ed.). Prensa de la Universidad de Cornell. p. 471., como se muestra en Página de Ken Brakke.
- ^ Frank, C. F.; Kasper, S. J. (1958), "estructuras de aleación complejo considerado como embalaje de la esfera. I. definiciones y principios básicos", Acta Crystallogr., 11. Frank, C. F.; Kasper, J. S. (1959), "estructuras de aleación complejo considerado como embalaje de la esfera. II. Análisis y clasificación de estructuras representativas", Acta Crystallogr., 12.
- ^ Fuente, Enrique (05 de agosto de 2008), "Un problema de burbujas Marcos un diseño olímpico", Tiempos de Nueva York.
Enlaces externos
- Modelos 3D de las estructuras de Weaire-Phelan, Kelvin y P42a
- Estructura de Weaire-Phelan desplegado dodecaedro y tetrakaidecahedron en PDF / formatos DXF
- Una imagen de la estructura de Weaire-Phelan
- Burbujas de Weaire-Phelan Página con ilustraciones y libremente descargable 'redes' para la impresión y fabricación de modelos.
- Superando a partición de Kelvin del espacio
- "Establecimiento de Weaire-Phelan espacio Modular inteligente", Alexandru Pintea, 2017, primer Premio Individual NASA Ames espacio solución concurso: