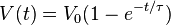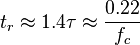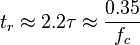Constante de tiempo RC

El Constante de tiempo RC, también llamada tau, es la constante de tiempo (en segundos) de un Circuito RC, es igual al producto de la resistencia del circuito (en ohmios) y el circuito capacitancia (en faradios), es decir,

\tau = R * C

Es el tiempo requerido para cargar el condensador, a través de la resistor, por ≈ 63,2 por ciento de la diferencia entre el valor inicial y final de valor o la descarga del condensador de ≈36.8 por ciento. Este valor se deriva de la constante matemática e, específicamente $1-e^{-1}$ , más específicamente como voltaje para cargar el condensador versus tiempo

Carga

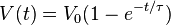V(t) = V_0(1-e^{-t/ \tau})

^[1]

Descarga

V(t) = V_0(e^{-t/ \tau})

Contenido

1 Frecuencia de corte
2 Retardo
3 Véase también
4 Referencias
5 Enlaces externos

Frecuencia de corte

La constante de tiempo $\tau$ se relaciona con la frecuencia de corte f_c, un parámetro alternativo del RC del circuito, por

\tau = RC = \frac{1}{2 \pi f_c}

o, equivalente,

f_c = \frac{1}{2 \pi R C} = \frac{1}{2 \pi \tau}

donde la resistencia en ohmios y la capacitancia en faradios rinde la constante de tiempo en segundos o en la frecuencia en Hz.

Cortas ecuaciones condicionales:

f _c en Hz = 159155 / τ en µs

Τ en µs = 159155 / f _c en Hz

Otras ecuaciones útiles son:

tiempo de subida (20% a 80%)

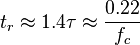
t_r \approx 1.4 \tau \approx \frac{0.22}{f_c}

tiempo de subida (10% a 90%)

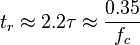
t_r \approx 2.2 \tau \approx \frac{0.35}{f_c}

Constantes de tiempo estándar y frecuencias de corte
para pre-pre-énfasis/de pre-énfasis RC Filtros:

Organización	Constante de tiempo $\tau$ en µs	F frecuencia de corte_c en Hz
RIAA	7958	20
RIAA, NAB	3183	50
—	1592	100
RIAA	318	500.5
—	200	796
—	140	1137
MC	120	1326
NAB	100	1592
MC	90	1768
RIAA, FM	75	2122
FM	50 / 75	2122 / 3183
NAB, PCM	50	3183
DIN	35	4547
—	25	6366
AES	17.5	9095
PCM	15	10610
—	12.5	12732
—	10	15915
Ortofon	3.5	45473
RIAA	3.18	50000

Más complicados circuitos que consta de más de un resistor o capacitor, la método constante circuito abierto proporciona una manera de aproximar la frecuencia de corte computando una suma de varias constantes de tiempo RC.

Retardo

El retraso de la señal de un alambre u otro circuito, medido como retardo de grupo o retardo de fase o el retardo de propagación efectiva de un digital transición, pueden ser dominados por los efectos capacitivos de resistiva, dependiendo de la distancia y otros parámetros, o alternativamente puede ser dominada por inductivo, onda, y velocidad de la luz efectos en otros reinos.

Resistiva capacitiva retraso o retardo RC, obstaculiza el mayor aumento de velocidad en Microelectrónica circuitos integrados. Cuando el tamaño de la función se convierte en más pequeño y más pequeñas para aumentar la velocidad de reloj, el retardo RC juega un papel cada vez más importante. Este retraso puede reducirse mediante la sustitución de la aluminio realización de alambre por cobre, reduciendo así la resistencia; también puede reducirse cambiando la capa intermediaria dieléctrico (generalmente dióxido de silicio) para materiales de baja constante dieléctrica, reduciendo así la capacitancia.

El retardo de propagación digital típico de un alambre resistente está sobre la mitad de R veces C; puesto que R y C son proporcionales a la longitud del cable, el retardo escala al cuadrado de la longitud del alambre. Carga se extiende por difusión en tal un alambre, como se ha explicado por Lord Kelvin a mediados del siglo XIX.^[2] Hasta Heaviside descubrió que Ecuaciones de Maxwell implica la propagación de la onda cuando suficiente inductancia está en el circuito, esta relación de difusión cuadrados fue pensada para proporcionar un límite fundamental para la mejora de los cables de telégrafo de larga distancia. Que viejo análisis fue reemplazado en el dominio del telégrafo, pero sigue siendo relevante para la en-viruta larga interconecta.^[3]^[4]^[5]

Véase también

Frecuencia de corte y respuesta de frecuencia
Énfasis, Preemphasis, deénfasis
Decaimiento exponencial
Filtro (procesamiento de señal) y función de transferencia
Filtro de paso alto, filtro de paso bajo, filtro paso banda
Circuito RL, y Circuito RLC

Referencias

^ https://Hyperphysics.PHY-astr.GSU.edu/HBase/Electric/capdis.html
^ Andrew Gray (1908). Lord Kelvin. Abolladura.
^ Ido Yavetz (1995). De la oscuridad a Enigma. Birkhäuser. ISBN3-7643-5180-2.
^ Jari Nurmi, Hannu Tenhunen, Jouni Isoaho y Axel Jantsch (2004). Diseño centrado en la interconexión avanzada SoC y NoC. Springer. ISBN1-4020-7835-8.
^ Scott Hamilton (2007). Un compañero de electrónica analógica. Cambridge University Press. ISBN0-521-68780-2.

Enlaces externos

Calculadora constante de tiempo RC
Constante de tiempo de conversión $\tau$ f frecuencia de corte_c y la parte posterior
Constante de tiempo RC

Otras Páginas

[1] ttps://Hyperphysics.PHY-astr.GSU.edu/HBase/Electric/capdis.html

[2] Andrew Gray (1908). Lord Kelvin. Abolladura.

[3] Ido Yavetz (1995). De la oscuridad a Enigma. Birkhäuser. ISBN3-7643-5180-2.

[4] Jari Nurmi, Hannu Tenhunen, Jouni Isoaho y Axel Jantsch (2004). Diseño centrado en la interconexión avanzada SoC y NoC. Springer. ISBN1-4020-7835-8.

[5] Scott Hamilton (2007). Un compañero de electrónica analógica. Cambridge University Press. ISBN0-521-68780-2.

﻿Constante de tiempo RC

﻿Contenido

﻿Frecuencia de corte

﻿Retardo

﻿Véase también

﻿Referencias

﻿Enlaces externos