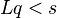Catástrofe de error

Catástrofe de error es la extinción de un organismo (a menudo en el contexto de microorganismos tales como virus) como resultado de mutaciones excesivas. Error catástrofe es algo predijo en modelos matemáticos y también se ha observado empíricamente.

Como todo organismo, virus 'equivocan' (o mutar) durante la replicación. Las mutaciones resultantes aumento biodiversidad entre la población y ayudarlos a subvertir la capacidad del sistema inmunológico de un huésped a reconocerlo en una infección posterior. Las mutaciones más el virus hace durante la replicación, más probable será evitar el reconocimiento por el sistema inmune y el más diverso de su población (ver el artículo sobre biodiversidad para una explicación de las ventajas selectivas de esto). Sin embargo si hace muchas mutaciones, puede perder algunas de sus características biológicas que han evolucionado a su ventaja, incluyendo su capacidad para reproducirse en absoluto.

Surge la pregunta: ¿Cuántas mutaciones pueden hacerse durante cada repetición antes de que la población de virus comienza a perder identidad?

Modelo matemático básico

Considere un virus que tiene una identidad genética modelada por una cadena de unos y ceros (por ejemplo 11010001011101...). Supongamos que la cadena ha longitud fija L y que durante la replicación del virus copias cada dígito uno por uno, cometiendo un error con probabilidad q independientemente de todos los otros dígitos.

Debido a las mutaciones resultantes de replicación errónea, existen hasta 2^L distintas cepas derivan de los virus de los padres. Dejar x_i denotan la concentración de tensión i; dejar a_i denotan la tasa a la cual cepa i reproduce; y dejar que Q_ij denota la probabilidad de que un virus de la cepa i mutando a cepa j.

A continuación, la tasa de cambio de concentración x_j está dada por

$\dot{x}_j = \sum_i a_i Q_{ij} x_i$

En este punto, hacemos una idealización matemática: elegimos la tensión más fuerte (el que tiene la mayor tasa de reproducción a_j) y asumir que es único (es decir, que los elegidos a_j satisface a_j > un_i para todos i); y luego agrupamos las cepas restantes en un solo grupo. Las concentraciones de los dos grupos sea x, y con tasas de reproducción a > b, respectivamente; dejar Q será la probabilidad de que un virus en el primer grupo (x) mutando a un miembro de la (segunda) grupoy) y R la probabilidad de que un miembro del segundo grupo volviendo a ser el primero (a través de una mutación muy específica y poco probable). Las ecuaciones que rigen el desarrollo de las poblaciones son:

$\begin{cases} \dot{x} = & a(1-Q)x + bRy \\ \dot{y} = & aQx + b(1-R)y \\ \end{cases}$

Estamos particularmente interesados en el caso donde L es muy grande, así que con seguridad podemos descuidamos R y en su lugar, considere:

$\begin{cases} \dot{x} = & a(1-Q)x \\ \dot{y} = & aQx + by \\ \end{cases}$

A continuación, ajuste z = x / y Tenemos

$\begin{matrix} \frac{\partial z}{\partial t} & = & \frac{\dot{x} y - x \dot{y}}{y^2} \\ && \\ & = & \frac{a(1-Q)xy - x (aQx + by)}{y^2} \\ && \\ & = & a(1-Q)z - (aQz^2 +bz) \\ && \\ & = & z(a(1-Q) -aQz -b) \\ \end{matrix}$.

Suponiendo que z alcanza una concentración constante en el tiempo, z se establece para satisfacer

$z(\infty) = \frac{a(1-Q)-b}{aQ}$

(que es deducido por el derivado de la configuración z con respecto al tiempo cero).

Entonces la pregunta importante es ¿bajo qué valores del parámetro persiste la población original (siguen existiendo)? La población persiste si y sólo si el valor de estado estacionario de z es estrictamente positivo. es decir, si y sólo si:

$z(\infty) > 0 \iff a(1-Q)-b >0 \iff (1-Q) > b/a .$

Este resultado más popular se expresa en términos de la relación de una: b y la tasa de error q de dígitos individuales: configurar b / a = (1-s), entonces se convierte en la condición

$z(\infty) > 0 \iff (1-Q) = (1-q)^L > 1-s$

Tomando un logaritmo a ambos lados y aproximar para pequeñas q y s uno consigue

$L \ln{(1-q)} \approx -Lq > \ln{(1-s)} \approx -s$

reducción de la condición de que:

$Lq < s$

Virus ARN que replicar cerca del umbral de error tienen un tamaño del genoma de orden 10⁴ pares de bases. Humano ADN se trata de 3.3 miles de millones (10⁹) base de unidades de largo. Esto significa que debe ser el mecanismo de replicación de ADN órdenes de magnitud más precisa que para el RNA.

Presentación de la información-teoría basada

Para evitar una catástrofe de error, la cantidad de información perdida a través de mutación debe ser menor que la cantidad obtenida mediante la selección natural. Este hecho puede utilizarse para llegar a esencialmente las mismas ecuaciones como la presentación más común de diferencial.

La información perdida puede ser cuantificada mediante la longitud del genoma L veces la tasa de error de replicación q. La probabilidad de supervivencia, S, determina la cantidad de datos aportados por la selección natural — y información es el registro negativo de probabilidad. Por lo tanto un genoma solo puede sobrevivir sin cambios cuando

$Lq < -\ln{S}$

Por ejemplo, el genoma muy sencillo donde L = 1 y q = 1 es un genoma con un bit que siempre muta. Desde Lq es 1, se deduce que S tiene que ser ½ o menos. Esto corresponde a la mitad la descendencia sobrevivir; es decir, la mitad con el genoma correcta.

Aplicaciones de la teoría

Algunos virus tales como poliomielitis o hepatitis C operar muy cerca de la tasa de mutación fundamental (es decir, el más grande q que L permitirá). Las drogas se han creado para aumentar la tasa de mutación de los virus para empujarlos sobre el límite crítico para que pierden identidad. Sin embargo, dada la crítica de la suposición básica del modelo matemático, este enfoque es problemático.

El resultado presenta un Catch-22 misterio para los biólogos: en general, son necesarios para la replicación exacta (replicación alta tasas se logran mediante la ayuda de grandes genomas enzimas), pero un gran genoma requiere una tasa de alta precisión q a persistir. ¿Que es lo primero y cómo sucede? Es una ilustración de las dificultades implicadas L Sólo puede ser 100 si q' es 0.99 - la longitud de una cadena muy pequeño en términos de genes.

Véase también

• Aceleración de la decadencia viral

Enlaces externos

• Estrategia de catástrofe y antiviral de error
• Aplicaciones de la catástrofe de error a la persistencia de cultivos transgénicos
• Teoría de las catástrofes de la Orgel Error del envejecimiento y la longevidad
• Examinar la teoría de la catástrofe de error

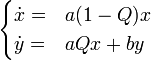
Otras Páginas

• Bathyphlebia
• Procurador legal
• Box Backup
• Cinturon de seguridad
• Ortoptica
• Tricromico
• Interes minoritario
• Seguros Parametricos
• DataPortability
• Blogshop
• Operaciones del negocio
• Lista de plantas utilizadas en herbolaria