Álgebra mediana
En matemáticas, un Álgebra mediana es un conjunto con un operación ternaria 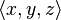 satisfacer un conjunto de axiomas que generalizar la noción de mediana o función de la mayoría, como un Función booleana.
satisfacer un conjunto de axiomas que generalizar la noción de mediana o función de la mayoría, como un Función booleana.
Los axiomas son
Los axiomas de segundo y terceros implica Conmutatividad:: es posible (pero no es fácil) para mostrar que en presencia de los otros tres, axioma (3) es redundante. El cuarto axioma implica la asociatividad. Existen otros sistemas axioma posible: por ejemplo los dos
también es suficiente.
En un Álgebra boleana, o más generalmente un enrejado distributiva, la función mediana  satisface los axiomas, así cada álgebra boleana y cada red distributiva forma una álgebra mediana.
satisface los axiomas, así cada álgebra boleana y cada red distributiva forma una álgebra mediana.
Birkhoff y beso que demostraron una álgebra mediana con elementos 0 y 1 satisfactorio < 0, x, 1 > = x es un enrejado distributiva.
Relación a los gráficos medianos
A gráfico de mediana es un gráfico sin señas en el cual por cada tres vértices x, y, y z Hay un único vértice < x, y, z > que pertenece a caminos más cortos entre cualquier par de x, y, y z. Si este es el caso, entonces la operación < x, y, z > define una álgebra mediana con los vértices de la gráfica como sus elementos.
Por el contrario, se puede definir en cualquier álgebra mediana, un intervalo [x, z] que el conjunto de elementos y tal que < x, y, z > = y. Se puede definir un gráfico de una álgebra mediana creando un vértice de cada elemento del álgebra y un borde para cada par (x, z) tal que el intervalo [x, z] no contiene otros elementos. Si el álgebra tiene la característica que cada intervalo es finito, entonces este gráfico es un medio gráfico, y representa con precisión el álgebra en eso la media operación definida por caminos más cortos en la gráfica coincide con operación mediana original de la álgebra.
Referencias
- Birkhoff, Garrett; Beso, S.A. (1947). "Una operación ternaria en enrejados distributivas". Toro. Amer. matemáticas. Soc. 53 (8): 749-752. Doi:10.1090/S0002-9904-1947-08864-9.
- Isbell, John R. (Agosto de 1980). "Álgebra mediana". Trans. Amer. matemáticas. Soc. (American Mathematical Society) 260 (2): 319-362. Doi:10.2307/1998007. JSTOR1998007.
- Knuth, Donald E. (2008). Introducción a los algoritmos combinatorios y funciones boleanas. The Art of Computer Programming 4.0. Upper Saddle River, NJ: Addison-Wesley. págs. 64 – 74. ISBN0-321-53496-4.
Enlaces externos
- Prueba de álgebra mediana
Otras Páginas
- John Simmons (abogado) (categoria de ley)
- Wellington da Silva Vicente
- Donal Reid
- Palm Centro
- Metodo de la participacion
- Sociedad Americana para la patologia investigadora
- Investigacion sobre la meditacion
- Hiperostosis cortical infantil
- Beca Thomas A. Scott en higiene
- Deglicirrizinado regaliz
- Samsung Galaxy Beam i8520
- Cobertura de contingente




